Introduction to Mathematical Reasoning
|
|
Fall 2016
| Lectures:
|
M-W-F
|
11:00 --11:50
|
Center 212
|
| Office Hour: |
M,F |
1:00 PM--2:00 PM |
APM 7230 |
|
W |
12:00 PM--1:00 PM |
APM 7230 |
| TA information: |
Jacob Postema |
jpostema ucsd ucsd  edu edu |
| TA Office hour: |
M |
12-2 pm |
T |
1:30-3:30 pm |
APM 6132 |
| TA information: |
Michelle Bodnar |
mbodnar ucsd ucsd  edu edu |
| TA Office hour: |
W |
1:00-3:00 pm |
F |
9:00-11:00 am |
APM 6434 |
|
Book
- Peter J. Eccles, An Introduction to Mathematical
Reasoning: numbers, sets, and functions. (The main textbook)
- R. B. Maddox, Mathematical Thinking and Writing: A
Transition to Abstract Mathematics.
- D. Smith, M. Eggen and R. St. Andre, A Transition to
Advanced Mathematics.
- D. Solow, How to Read and Do Proofs.
|
| Schedule
This is a tentative schedule for the course. If necessary, it
may change.
|
| Homework
- Homework are due on Wednesdays at 5:00 pm. You should drop
your homework assignment in the homework drop-box in the basement of
the AP&M building.
- Late Homework are not accepted.
- There will be 9 problem sets. Your cumulative homework
grade will be based on the best 8 of the 9.
- If your homework is typed and well-written (based on the grader's judgement), its score will be multiplied by 1.1!
- You can work on the problems with your classmates, but you have to write down your own version.
Copying from other's solutions is not accepted and is considred cheating.
- A good portion of the exams will be based on the weekly problem sets.
So it is extremely important for you to make sure that you understand each one of them.
|
| Grade
- Your weighted score is the best of
- Homework 20%+ midterm exam I 20%+ midterm exam II 20%+ Final 40%
- Homework 20%+ The best of midterm exams 20%+ Final 60%
- Your letter grade is determined by your weighted score
using the best of the following methods:
-
| A+ |
A |
A- |
B+ |
B |
B- |
C+ |
C |
C- |
| 97 |
93 |
90 |
87 |
83 |
80 |
77 |
73 |
70 |
- Based on a curve where the median
corresponds to the cut-off B-/C+.
|
Regrade
- Homework and midterm exams will be returned in the discussion sections.
- If you wish to have your homework or exam regraded, you must return it immediately to your TA.
- Regrade requests will not be considered once the homework or exam leaves the room.
- If you do not retrieve your homework or exam during discussion section,
you must arrange to pick it up from your TA within one week after it was
returned in order for any regrade request to be considered.
|
Further information
- There is no make-up exam.
- Keep all of your returned homework and exams.
If there is any mistake in the recording of your scores, you will need the original assignment in order for us to make a change.
- No notes, textbooks, calculators and electronic devices are allowed during exams.
- You must bring a blue book to the exam.
|
| Exams.
- The first exam:
- Time: Tuesday, October 18, 18:30-19:20.
- Location: Students in A01 and A02 should go to room Center 109; Students in A03 and A04 should go to room HSS 1330.
I am not happy about the fact that these rooms are not close to each other and you have to
go to a different room as our usual place, but these are the rooms that university
could provide for us! So please locate these room prior to the exam.
- Topics: All the topics that are discussed in class and relevant chapters of your book till end of strong induction.
- Questions are fairly similar to the homework assignments
and the examples discussed in the class. Make sure that you know how to solve anyone of them.
- Practice: You should first study the lecture notes, then go through
the homework assignments, after that study examples mentioned in your book, and the relevant problems in your book.
You might find these problems useful.
Here is an old first-exam, and
here
is its solution. Here is another exam.
- Exam: Here is the exam.
- Here is the frequency of your grades.
-
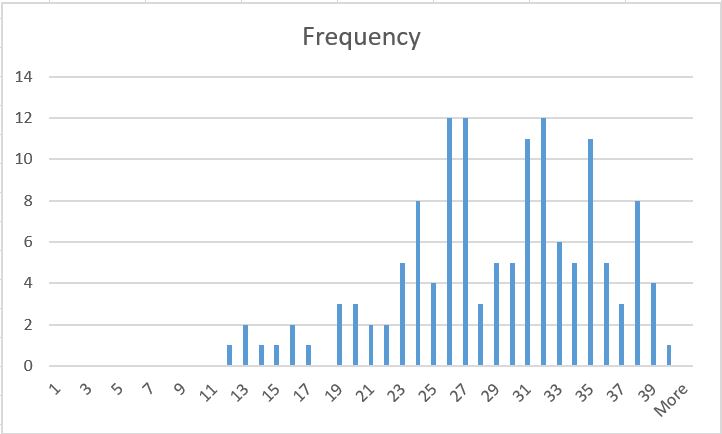
-
Overall grades look OK! I expected a bit better performance from you.
-
The median is 30.
-
I am really happy to see that there are 5 students who got 39 and above. I would like to congratulate and thanks them for their effort.
-
If you have got 20 or under, this should be extremely alarming for you.
You should reconsider your approach towards this course entirely.
-
No letter grade is assigned to the midterm exams. At the end of the quarter according to the syllabus, your numerical
grades in exams 1 and 2 will be used to compute your weighted score. Then your wieghted score will be used
to assign your letter grades.
- The second exam:
- Time: Tuesday, November 15, 18:30-19:20.
- Location: Students in A01 and A02 should go to room Center 109; Students in A03 and A04 should go to room HSS 1330.
I am not happy about the fact that these rooms are not close to each other and you have to
go to a different room as our usual place, but these are the rooms that university
could provide for us! So please locate these room prior to the exam.
- Topics: All the topics that are discussed in class and relevant chapters of your book till end of
bijection and invertibility (end of lecture 21).
- Questions are fairly similar to the
homework assignments and the examples discussed in the class. Make sure
that you know how to solve anyone of them.
- Extra help:
-
You may find this practice sheet helpful.
Here is a past exam, and Here
is its solution.
- Exam: Here is the exam.
- Here is the frequency of your grades.
-
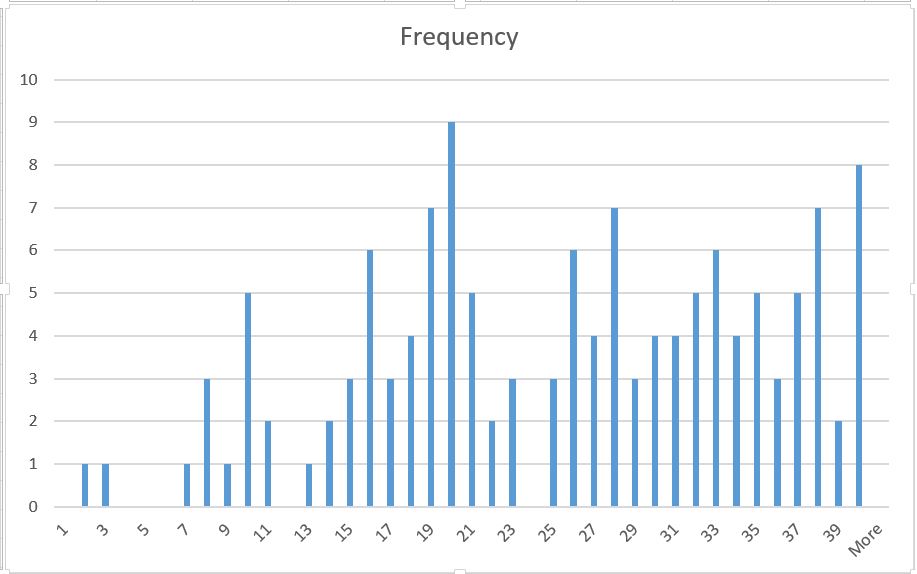
-
I was shocked to see such a low performance! The median was 26.
-
I am really happy to see that there are 10 students who got 39 and above.
I would like to congratulate and thanks them for their effort.
The final exam:
- Date: Tuesday, December 6, 11:30 am- 2:29 pm.
- Location:
- Students from discussion sections A01, A02, and A03 should go to room Center 212.
- Students from discussion section A04 should go to room PCYNH 120.
- Notice that these are NOT the same rooms as
the ones that we used for the previous exams. Please locate them prior to the exams.
- Topics: All the topics that were discussed in class, your homework assignments, and relevant examples and exercises in the
practice exercises and your book.
- Questions are fairly similar to the
homework assignments and the examples discussed in the class. Make sure
that you know how to solve anyone of them.
- Extra help:
-
You may find this set of
practice problems useful. I admit
that some of these problems are hard, but nevertheless they are
good for your practice.
-
You may find the posted extra problem set and the main ideas of its solution useful.
-
I will hold an extended office hour: Monday, 12/5/2016, 1:00 pm- 4:00 pm.
|
| Assignments.
Problem sets will be posted here. Make sure to refresh your borwser.
I would like to thank Michelle Bodnar for providing the HW solutions.
- Due October 5: Here is the first problem set. Here is its solution.
- Due October 12: Here is the second problem set. Here is its solution.
- Due October 19: Here is the thrid problem set. Here is its solution.
- Due October 26: Here is the fourth problem set. Here is its solution. (For 5.b, you can use 3.c as well.)
- Due November 2: Here is the fifth problem set. Here is its solution.
- Due November 9: Here is the sixth problem set. Here is its solution.
- Due November 16: Here is the seventh problem set. Here is its solution.
- Due November 23: Here is the eighth problem set. Here is its solution.
- For your own practice: Here is an extra problem set
with solutions with not much details.
|
| My notes.
I will post my notes here. You are supposed to read these notes and the relevant chapters of your book.
You might find my notes from Fall 2015 useful: Here is a link to the webpage of that class.
- Lecture 1: Propositions here is my note.
- Lecture 2: Propositional forms and truth table here is my note.
- Lecture 3: Equivalent forms of an implication. How to prove two propositional forms are equivalent without using truth table. Divisibility.
here is my note.
-
Lecture 4: Linear Diophantine equations, odd/even, and biconditional propositions. here is my note.
-
Lecture 5: Odd/even, what prime is, 2 is prime, inequality. here is my note.
-
Lecture 6: Basic properties of absolute value, unofficial introduction to induction: sum of the first n positive odd numbers, what is sqrt(2+sqrt(2+sqrt(2+...) ))? here is my note.
-
Lecture 7: Induction principle and the formal proof of the previously discussed examples. here is my note.
-
Lecture 8: Various properties of Fibonacci sequence. here is my note.
-
Lecture 9: Binet formula, strong induction, and how diagonalizing can help. here is my note.
-
Lecture 10: Irreducible numbers and factorizing to irreducible numbers using strong induction. here is my note.
-
Lecture 11: Language of set theory (and review). here is my note.
-
Lecture 12: Power set, (intuitive) cardinality (for finite sets), Venn diagram, and set operations. here is my note.
-
Lecture 13: Properties of set operations and introduction to quantifiers. here is my note.
-
Lecture 14: Quantifiers. (0,1) has no minimum. Basics of game theory and its connection with quantifiers. here is my note.
-
Lecture 15: Quantifiers and epsilon-delta definition of limit. here is my note.
-
Lecture 16: Quantifiers and how to show a limit does not exist. here is my note.
-
Lecture 17: Cartisian product, functions, and composition of functions. here is my note.
-
Lecture 18: Identity function, composition of functions, image of a function, surjective functions. here is my note.
-
Lecture 19: Surjective, injective and bijective functions. here is my note.
-
Lecture 20: Connections between surjection, injection, and composition of functions; invertible functions. here is my note.
-
Lecture 21: Having left inverse iff injective; Having right inverse iff surjective;
Invertible iff bijective; Axiom of choice. here is my note.
-
Lecture 22: Inverse of a bijection; composition of bijections; equipotent sets; cardinality of a set;
pigeonhole principle (without proof). here is my note.
-
Lecture 23: Enumerable sets; Hilbert's hotel; Z is enumerable; Z+xZ+ is enumerable. here is my note.
-
Lecture 24: Cardinality of a set; aleph0; Cantor's theorem |X|<|P(X)|; Cantor's diagonal argument: |R|> |Z|. here is my note.
-
Lecture 25: The floor function; Division algorithm. here is my note.
-
Lecture 26: Congruence arithmetic; connection between Division algorithm and conguences; remainder of a division by 9 or 11. here is my note.
-
Lecture 27: Pigeonhole and divisibility;
the greatest common divisor of a and b can be written as an integer linear combination of a and b; (gcd(a,b)=1 and a|bc) implies a|c. here is my note.
-
Lecture 28: Prime if and only if irreducible; equations in congruence arithemtic; a ≡ b (mod n) implies gcd(a,n)=gcd(b,n). here is my note.
-
Lecture 29: ax≡ b (mod n) has a solution if and only if gcd(a,n)|b;
a has a modular arithmetic modulo n if and only if gcd(a,n)=1; Euclid's algorithm; How to find integers x and y such that ax+by=gcd(a,b). here is my note.
|

 ucsd
ucsd  edu
edu