Calculus for science and engineering III (Lecture B)

Fall 2016

Lectures: M-W-F 10:00 PM--10:50 AM Peter 110
Office Hour: M,F 12:00 PM--1:00 PM APM 7230

W 1:00 PM--2:00 PM APM 7230

Discussion sessions information:

B01   W 7:00 PM--7:50 PM   APM B402A   Anirudh Ravichandran   anravichucsd edu
B02   W 8:00 PM--8:50 PM   APM B402A   Anirudh Ravichandran   anravichucsd edu
B03   W 5:00 PM--5:50 PM   CSB 005   Juan Sidrach De Cardona Mora   jsidrachucsd edu
B04   W 6:00 PM--6:50 PM   CSB 005   Juan Sidrach De Cardona Mora   jsidrachucsd edu
B05   W 7:00 PM--7:50 PM   CSB 005   Juan Sidrach De Cardona Mora   jsidrachucsd edu
B06   W 8:00 PM--8:50 PM   CSB 005   Juan Sidrach De Cardona Mora   jsidrachucsd edu
B07   W 6:00 PM--6:50 PM   Center 220   Xin Tong   xit040ucsd edu
B08   W 7:00 PM--7:50 PM   Center 220   Xin Tong   xit040ucsd edu
B09   W 8:00 PM--8:50 PM   Center 220   Kirstyn Gunaji   kgunajiucsd edu
B10   W 9:00 PM--9:50 PM   Center 220   Kirstyn Gunaji   kgunajiucsd edu

TA's office hours information:

Juan Sidrach De Cardona Mora M 3-5pm APM 2402A
Juan Sidrach De Cardona Mora M 5-7pm Calc. Lab, APM B402a
Kirstyn Gunaji T 8-9pm APM 2313
Kirstyn Gunaji T 9-10pm Cal Lab, APM B402a
Xin Tong Th 9-11am APM 6414
Anirudh Ravichandran T 9:30-10:30am APM 2313
Anirudh Ravichandran F 7-8pm APM 2313

General information     Book     Calendar     Homework     Grade     Regrade     Exams     Assignment
General information

  • Title: Calculus for Science and Engineering.
  • Credit Hours: 4 (2 credits if taken after Math 10C).
  • Prerequisite: AP Calculus BC score of 3, 4, or 5; or, Math 20B with a grade of C- or better.
  • Catalog Description: Vector geometry, vector functions and their derivatives. Partial differentiation. Maxima and minima. Double integration.
Book

  • J. E. Marsden, A. Tromba, Vector Calculus (6th edition), Published by W.H.Freeman and Company, 2012.
  • This is the same book as the one used in Math 20E.
  • We will cover parts of Chapters 1-5 of the text. Math 20E covers almost everything else in text.
Schedule

This is a tentative schedule for the course. If necessary, it may change.

Homework

  • Homework will be assigned in the assignment section of this page.
  • Homework assignments are due on Thursdays at 5:00 pm. You should drop your homework assignments in the homework drop-box in the basement of the AP&M building.
  • Late homework is not accepted.
  • There will be 9 problem sets. Your cumulative homework grade will be based on the best 8 of the 9.
  • Selected problems on the each assignment will be graded.
  • Style:
    • A messy and disorganized homework might get no points.
    • The upper right corner of each assignment must include:
      1. Your name (last name first).
      2. Your discussion session (e.g. B01,etc.).
      3. Homework assignment number.
    • Full-sized notebook papers should be used.
    • All pages should be stapled together.
    • Problems should be written in the same order as the assignment list. Omitted problems should still appear in the correct order.
  • A good portion of the exams will be based on the weekly problem sets. So it is extremely important for you to make sure that you understand each one of them.
  • You can work on the problems with your classmates, but you have to write down your own version. Copying from other's solutions is not accepted and is considered cheating.
  • In addition to the discussion section and your TA's and instructor's office hours, you can get help with the homework assignments in the Calculus Tutoring Lab (AP&M B402A).
  • Reading the sections of the textbook corresponding to the assigned homework exercises is considered part of the homework assignment. You are responsible for material in the assigned reading whether or not it is discussed in the lecture.
  • Homework will be returned in the discussion sections.
Grade

  • Your weighted score is the best of
    • Homework 20%+ midterm exam I 20%+ midterm exam II 20%+ Final 40%
    • Homework 20%+ The best of midterm exams 20%+ Final 60%
  • You must pass the final examination in order to pass the course.
  • Your letter grade is determined by your weighted score using the best of the following methods:
    • A+ A A- B+ B B- C+ C C-
      97 93 90 87 83 80 77 73 70
    •  Based on a curve where the median corresponds to the cut-off B-/C+.
  • If more than 90% of the students fill out the CAPE questioner at the end of the quarter, all the students get one additional point towards their weighted score.
Regrade
  • Homework and midterm exams will be returned in the discussion sections.
  • If you wish to have your homework or exam regraded, you must return it immediately to your TA.
  • Regrade requests will not be considered once the homework or exam leaves the room.
  • If you do not retrieve your homework or exam during discussion section, you must arrange to pick it up from your TA within one week after it was returned in order for any regrade request to be considered.
Further information
  • There is no make-up exam.
  • Keep all of your returned homework and exams. If there is any mistake in the recording of your scores, you will need the original assignment in order for us to make a change.
  • No notes, textbooks, calculators and electronic devices are allowed during exams.
  • You must bring a blue book to the exam.
  • Calculus Tutoring Lab: A tutoring lab for Calculus students will generally be open Monday through Friday, 9:00am - 5:00pm in APM B402; There will usually be at least 2 tutors and/or TAs available to help with homework, calculators, and coursework. We strongly recommend that you make use of the Calculus Tutoring Lab.
  • For homework, you may use any handheld graphing calculator. The TI-83 Plus, TI-84 Plus or similar calculators are suitable. More powerful calculators with a built-in CAS, such as a TI-89, should only be purchased if you expect to need it for your future work. Please Note: Calculators will not be allowed on exams.
  • Academic Dishonesty: Academic dishonesty is considered a serious offense at UCSD. Students caught cheating will face an administrative sanction which may include suspension or expulsion from the university. It is in your best interest to maintain your academic integrity.
Exams.

  • The first exam:
    • Time: Tuesday, October 18, 20:00-20:50.
    • Location: Students in B01, B02, B03 should go to room Center 113, and Students in B04, B05, B06, B07, B08, B09, B10 should go to room Peter 110. I am not happy about the fact that these rooms are not close to each other and you have to go to a different room as our usual place, but these are the rooms that university could provide for us! So please locate these room prior to the exam.
    • You may bring one 8.5 by 11 inch sheet of notes (which may be written on both sides) with you.
    • No calculators will be allowed during the final examination.
    • Topics: All the topics that are discussed in the class and in the book about Sections 1.1, 1.2, 1.3, 2.1, 2.2.
    • Questions are fairly similar to the homework assignments and the examples discussed in the class. Make sure that you know how to solve anyone of them.
    • Practice: besides going through your homework assignments, examples presented in the class and problems in the relevant chapters of your book, you can use the following "practice exams". There are caveats associated with these. They are exams from 2013 and 2014, and at that time a different book and syllabus were used. Nevertheless, I thought it is good for you to have them as a resource:
    • You will need a blue book.
    • Here is the version one of the first exam. Here is its solution.
    • Here is the frequency of your grades.
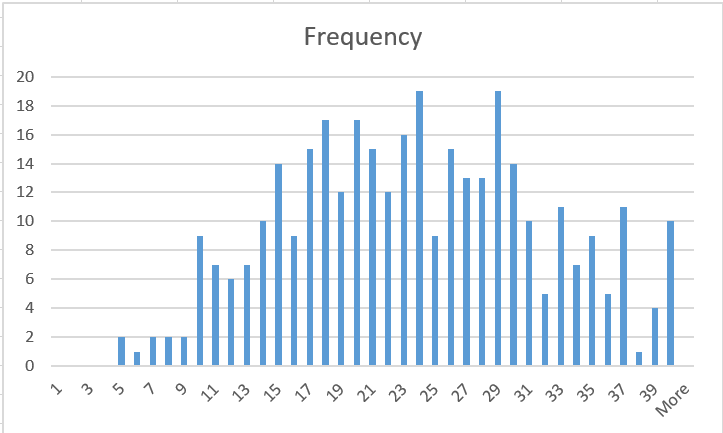
    • This exam was out of 37 with a 3-point bonus problem. The median was 23.25.
    • It goes without saying that I am absolutely shocked. I expected a much better performance from you.
    • If you have got 16 or under, this should be extremely alarming for you. You should reconsider your approach towards this course entirely.
    • I am really happy to see that there are 22 students who got 37 and above. I would like to congratulate and thanks them for their effort.
    • No letter grade is assigned to the midterm exams. At the end of the quarter according to the syllabus, your numerical grades in exams 1 and 2 will be used to compute your weighted score. Then your wieghted score will be used to assign your letter grades.
  • The second exam:
    • Time: Tuesday, November 15, 20:00-20:50.
    • Location: Students in B01, B02, B03 should go to room Center 113, and Students in B04, B05, B06, B07, B08, B09, B10 should go to room Peter 110. I am not happy about the fact that these rooms are not close to each other and you have to go to a different room as our usual place, but these are the rooms that university could provide for us! So please locate these room prior to the exam.
    • Rule 1: You may bring one 8.5 by 11 inch sheet of notes (which may be written on both sides) with you to the exam.
    • Rule 2: No calculators will be allowed during the exam.
    • Topics: All the topics that are discussed in the class and in the book about Sections 1.1, 1.2, 1.3, 2.1, and 2.2, 2.3, 2.4, 2.5, 2.6, 3.1, 3.3. The emphasis will be given to the second part.
    • Questions are fairly similar to the homework assignments and the examples discussed in the class. Make sure that you know how to solve anyone of them. And go over the lecture notes I have posted online.
    • Practice: besides going through your homework assignments, examples presented in the class and problems in the relevant chapters of your book, you can use the following "practice exams". There are caveats associated with these. They are exams from 2013 and 2014, and at that time a different book and syllabus were used. Nevertheless, I thought it is good for you to have them as a resource:
    • You will need a blue book.
    • Here is the version one of the first exam. Here is its solution.
    • Here is the frequency of your grades.
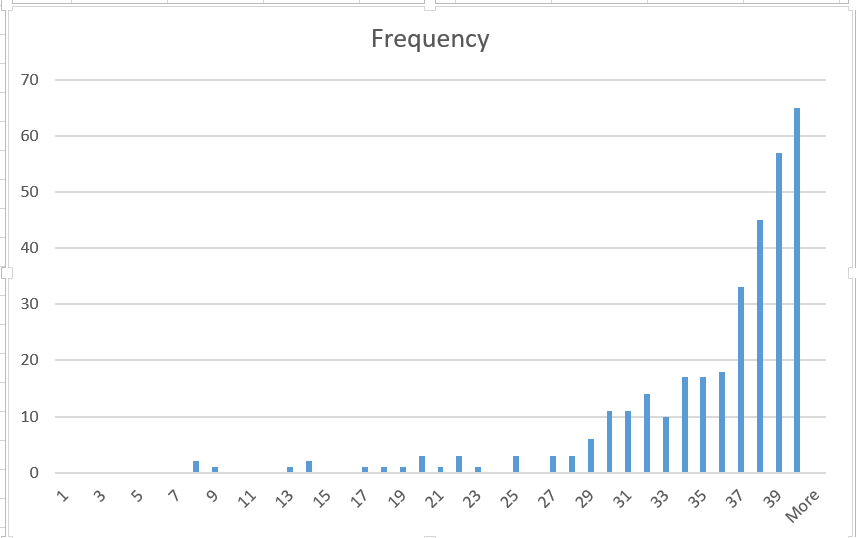
    • This exam was out of 40. The median was 37.5.
    • It was a joy to see such a great performance.
  • The final exam:
    • Time: Friday, December 9, 8:00 am- 10:59 am
    • Location:
      • Students from sections B01, B02, and B03 should go to the room Center 214.
      • Students from sections B04, B05, B06, B07, B08, B09, and B10 should go to the room Peter 110.
      • Notice that we are using a different room as the one used for the previous exams. Please locate it before the final exam.
    • Rule 1: It is your responsibility to ensure that you do not have a schedule conflict involving the final examination. You should not enroll in this class if you cannot sit for the final examination at its scheduled time.
    • Rule 2: You may bring one 8.5 by 11 inch sheet of notes (which may be written on both sides) with you to the final examination.
    • Rule 3: You should bring a blue book.
    • Rule 4: You should bring your student ID.
    • Rule 5: No calculators will be allowed during the final examination.
    • Topics: All the topics that are discussed in the class and in the relevant sections of book.
    • Questions are fairly similar to the homework assignments and the examples discussed in the class. Make sure that you know how to solve anyone of them.
    • Practice: besides going through your homework assignments, examples presented in the class and problems in the relevant chapters of your book, you can use the following "practice exams". There are caveats associated with these. They are exams from 2013 and 2014, and at that time a different book and syllabus were used. Nevertheless, I thought it is good for you to have them as a resource:
    • As it is stated above, in the worst case scenario the median of the weighted scores corresponds to the B-/C+ cut-off.
    • I will hold an office hour on Wednesday, 12/7/2016, 1:00 pm-4:00 pm.
Lectures
Sometimes I put the summary of the lectures here. These are just the headlines of the topics that we discussed in the class, and you should read your book to understand the covered topics.
  • Lecture 1: geometric and algebraic interpretations of vectors. Here is my note.
  • Lecture 2: 3D vectors, standard basis, parallel vectors, a moving particle with constant velocity. Here is my note.
  • Lecture 3: parametrizations of lines, midpoints, inner product. Here is my note.
  • Lecture 4: inner product, length and direction of a 3D vector, geometric properties of inner product. Here is my note.
  • Lecture 5: Geometric applications of inner product, orthogonal projection, determinant of 2x2 matrices. Here is my note.
  • Lecture 6: Determinant of 3x3, cross product, algebraic and geometric properties of cross product. Here is my note.
  • Lecture 7: Geometric properties of cross product, Right-hand rule, area of a parallelogram, area of a triangle, volume of a parallelepiped. Here is my note.
  • Lecture 8: How to find an equation of a plane in various settings, distance of a point from a plane. Here is my note.
  • Lecture 9: Multi-variable functions: their domain, graph, and contour curves. Here is my note.
  • Lecture 10: Level surfaces and limits of multivariable functions. Here is my note.
  • Lecture 11: Limits: approaching along curves other than lines, squeeze theorem, polar coordinates. Here is my note.
  • Lecture 12: Limits: polar coordinates, partial derivatives: how to compute and their geometric interpretation. Here is my note.
  • Lecture 13: Tangent plane, affine approximation of a function, and differentiability. Here is my note.
  • Lecture 14: Differentiation, approximation. Here is my note.
  • Lecture 15: Vector-valued functions: limit, derivative; Velocity, Acceleration, Speed; Tangent line of a curve. . Here is my note.
  • Lecture 16: Parametrization of a curve, chain rule. Here is my note.
  • Lecture 17: Chain rule; gradient and their connections with level curve, level surfaces and their tanget planes. Here is my note.
  • Lecture 18: More on tangent planes of level surfaces. Directional derivatives. Here is my note.
  • Lecture 19: Properties of directional derivatives, chain rule (the general case), implicit differentiation. Here is my note.
  • Lecture 20: Iterated partial derivatives, local max, local min, critical , and saddle points. Here is my note.
  • Lecture 21: The 2nd order derivative test. Bounded and closed regions. Here is my note.
  • Lecture 22: Global max and min; Lagrange multiplier method. Here is my note.
  • Lecture 23: Lagrange multiplier method. Here is my note.
  • Lecture 24: Lagrange multiplier method; regular points of a curve. Here is my note.
  • Lecture 25: Anti-derivative of a vector-valued function; acceleration, velocity, positional vector; total distance traveled; arc-length; arc-length function. Here is my note.
  • Lecture 26: Double integral; Fubini's theorem; iterated integrals; changing the order of integration. Here is my note.
  • Lecture 27: Double integral over more general regions; Switching the order of integration. Here is my note.
  • Lecture 28: Order of integration; volume of solids; polar coordinstes. Here is my note.
  • Lecture 29: Polar coordinates and double integrals; volume of solids. Here is my note.

Here are some notes from 2014. A different book and syllabus were used at that time, but you might still find them useful:
Assignments
The list of homework assignments are subject to revision during the quarter. Please check this page regularly for updates. (Do not forget to refresh your page!)
  • Homework 1 (Due October 6)
    • Section 1.1: 4, 6, 9, 13, 15, 16, 18, 23, 24, 27, 37.
    • Section 1.2: 1, 2, 3, 7, 9, 13, 15, Normalize the vectors in Exercise 6, 19, 20, 22, 24, 26, 29.

  • Homework 2 (Due October 13)
    • Section 1.3: 2(a), 2(b), 2(c), 3, 4, 5, 6, 7, 10, 15(b), 15(d), 16(a), 16(c), 26, 28, 31, 33, 34.

  • Homework 3 (Due October 20)
    • Section 2.1: 3, 5, 7, 13, 20, 21, 25, 27, 31, 37, 38.
    • Section 2.2: 6, 8, 10, 15, 25(a), 25(b).

  • Homework 4 (Due October 27)
    • Section 2.3: 1, 3, 5, 7, 11, 12, 17, 21, 24.

  • Homework 5 (Due November 3)
    • Section 2.4: 1, 4, 5, 6, 8, 10, 12, 13, 18, 20, 23.
    • Section 2.5: 3, 10, 13, 33, 35.
    • Look through Review Exercises for Chapter 2: 9, 10, 14, 17, 19, 33. (These will not be turned in).

  • Homework 6 (Due November 10)
    • Section 2.5: 9, 19(c), 32.
    • Section 2.6: 2, 3(a), 4, 6, 7, 8, 9(a), 20.
    • Section 3.1: 1, 3, 6, 9, 11, 21(a), 25.

  • Homework 7 (Due November 17)
    • Section 3.3: 1, 2, 4, 7, 17, 19, 20, 28.
    • Section 3.4: 1, 3, 4, 7, 13, 19, 20, 21.
      • Note: Skip "A Second Derivative Test for Constrained Extrema" (pg 197 - 201)
    • Section 4.1: 1, 2, 9.

  • Homework 8 (Due November 23, 5 pm) (The due time is changed and the number of problems is reduced because of Thanksgiving.)
    • Section 4.1: 11, 12, 14.
    • Section 4.2: 1, 3, 4, 10.

  • Homework 9 (Due December 1)
    • Section 5.1: 1, 3, 6, 9, 13, 14, 15.
    • Section 5.2: 1(c), 3, 5, 8, 11.
    • Section 5.3: 1, 2, 3, 4(a), 4(c), 13, 17.

  • Homework 10 (NOT Due)
    • Section 5.4: 1, 2, 5, 12, 14.
    • Section 5.5: 1, 3, 11, 13, 19, 23.
    • Section 1.4: 3(a), 8(a).
    • Section 6.2: 3, 11, 13, 15.
Acknowledgement. I would like to thank the previous instructors of Math 20C for providing their course webpages and exams available for public. The following pages were instrumental in the preparation of the materials of this page: