Introduction to Mathematical Reasoning
|
|
Fall 2015
| Lectures:
|
M-W-F
|
12:00 --12:50
|
Center 216
|
| Office Hour:
|
W,F
|
1:00 PM--2:30 PM
|
APM 7230 |
| TA information: |
Ching Wei Ho |
cwho ucsd ucsd  edu edu |
| TA Office hour: |
M |
3:00-5:00 |
W |
3:00-5:00 |
APM 6351 |
| TA information: |
Peter Wear |
pwear ucsd ucsd  edu edu |
| TA Office hour: |
W |
3:30-5:30 |
Th |
10:00-12:00 |
APM 6446 |
|
Book
- Peter J. Eccles, An Introduction to Mathematical
Reasoning: numbers, sets, and functions. (The main textbook)
- R. B. Maddox, Mathematical Thinking and Writing: A
Transition to Abstract Mathematics.
- D. Smith, M. Eggen and R. St. Andre, A Transition to
Advanced Mathematics.
- D. Solow, How to Read and Do Proofs.
|
| Schedule
This is a tentative schedule for the course. If necessary, it
may change.
|
| Homework
- Homework are due on Fridays at 5:00 pm. You should drop
your homework assignment in the homework drop-box in the basement of
the AP&M building.
- Late Homework are not accepted.
- There will be 8 problem sets. Your cumulative homework
grade will be based on the best 7 of the 8.
- If your homework is typed and well-written (based on the grader's judgement), its score will be multiplied by 1.1!
- You can work on the problems with your classmates, but you have to write down your own version.
Copying from other's solutions is not accepted and is considred cheating.
- A good portion of the exams will be based on the weekly problem sets.
So it is extremely important for you to make sure that you understand each one of them.
|
| Grade
- Your weighted score is the best of
- Homework 20%+ midterm exam I 20%+ midterm exam II 20%+ Final 40%
- Homework 20%+ The best of midterm exams 20%+ Final 60%
- Your letter grade is determined by your weighted score
using the best of the following methods:
-
| A+ |
A |
A- |
B+ |
B |
B- |
C+ |
C |
C- |
| 97 |
93 |
90 |
87 |
83 |
80 |
77 |
73 |
70 |
- Based on a curve where the median
corresponds to the cut-off B-/C+.
|
Regrade
- Homework and midterm exams will be returned in the discussion sections.
- If you wish to have your homework or exam regraded, you must return it immediately to your TA.
- Regrade requests will not be considered once the homework or exam leaves the room.
- If you do not retrieve your homework or exam during discussion section,
you must arrange to pick it up from your TA within one week after it was
returned in order for any regrade request to be considered.
|
Further information
- There is no make-up exam.
- Keep all of your returned homework and exams.
If there is any mistake in the recording of your scores, you will need the original assignment in order for us to make a change.
- No notes, textbooks, calculators and electronic devices are allowed during exams.
- You must bring a blue book to the exam.
|
| Exams.
- The first exam:
- Topics: All the topics that are discussed in the
class and in the book till the end of strong induction. I have decided to NOT include the set theory
in the first exam.
- Questions are fairly similar to the homework assignments
and the examples discussed in the class. Make sure that you know how to solve anyone of them.
- Practice: You should first study the lecture notes, then go through
the homework assignments, after that study examples mentioned in your book, and the relevant problems in your book.
You might find these problems useful.
Here is an old first-exam, and
here
is its solution.
- Exam: Here is the first exam.
-
Here is the frequency of the scores.
-
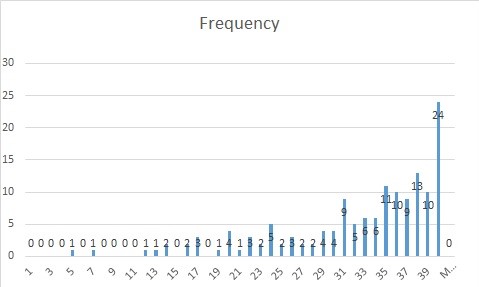
-
Of course I am extremely happy about the large number (34 out of 150) of students
who got at least 39, but at the same time I am extremely worried about the large number (35 out of 150) of you who got
less than 28.
-
If your score is less than 28 and more than 20, this should be an alarming sign for you. You should find out why you did not perform well
and how you can improve.
-
If your score is at most 20, then you need to seriously reconsider your approach towards this course.
If you continue the same way, most likely you would fail the course.
- The second exam:
- Topics: All the topics that are discussed in the
class and in the book on set theory, quantifiers, limit, games, functions. (From set theory to the end of the topics covered by November 13,
including the lecture on Friday.) You might need the concepts discussed earlier indirectly.
- Questions are fairly similar to the
homework assignments and the examples discussed in the class. Make sure
that you know how to solve anyone of them.
- Extra help:
-
Peter Wear will be holding an extra office hour on Tuesday, Nov. 17, 12-2. I encourage you to take advantage of this
oppurtunity.
-
I will be holding an extra office hour on Monday 1:00-2:30.
-
You may find this practice sheet helpful.
- Overflow exam room: If you are enrolled in A01,
then you should go to Pepper Canyon Hall 120 (PCYNH 120).
- Exam: Here is the second exam. And Here
is its solution.
-
Here is the frequency of the scores.
-
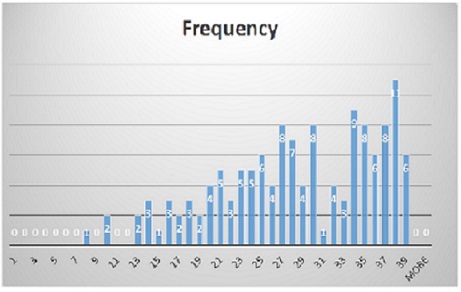
-
I expected a much better performance. Hopefully you will do much better in the final exam.
- The final exam:
- Topics: All the topics that were discussed in class, your homework assignments, and relevant examples and exercises in the
practice exercises and your book.
- Questions are fairly similar to the
homework assignments and the examples discussed in the class. Make sure
that you know how to solve anyone of them.
- Extra help:
-
Ching Wei Ho will be holding an extra office hour on Wednesday, December 9, 3-5. I encourage you to take advantage of this
oppurtunity. (By the way this would be your last chance to pick up your HW and midterms.)
-
I will be holding an extra office hour on Monday 9:00-11:00. It will be in the room APM B412. Please come prepared with your questions.
-
You may find this set of practice problems useful. I admit that some of these problems are hard, but nevertheless they are
good for your practice.
- Overflow exam room: If you are enrolled in A03,
then you should go to Center Hall 222.
|
| Assignments.
- Due October 9: Here is the first problem set. Here is its solution.
- Due October 16: Here is the second problem set. Here is its solution.
- Due October 23: Here is the third problem set. Here is its solution.
- Due October 30: Here is the forth problem set. Here is its solution.
- Due November 6: Here is the fifth problem set. Here is its solution.
- Due November 13: Here is the sixth problem set. Here is its solution.
- Due November 20: Here is the seventh problem set. Here is its solution.
- Due December 4: Here is the eighth problem set. Here is its solution.
- For your own practice: Here is the ninth problem set.
|
My notes.
-
In the first lecture,
we talked about the goals of this course, mathematical language, proposition, predicate, free variables, logical connectives,
quantifiers, negation, and truth table.
-
In the second lecture,
we talked about Russell type of sentences, case-by-case proof, proof by contradiction,
propositional forms, equivalent propositions, de Morgan's law, conditional proposition/implication.
-
In the third lecture, we learned about contrapositive and
converse of an implication. We saw that the contrapositive implication is equivalent to the original proposition, but not
the converse implication. We used a Kenken game to practice case-by-case proof and proof by contradiction. We discussed divisibility,
and proved two easy properties using direct proof and proof by contradiction.
-
In the forth lecture, we went through implications again,
proved some results related to divisibility, introduced biconditional propositions, and siad what Theorem,
Proposition, Lemma, Corollary, Definition, and Remark mean in math books and articles. We also pointed out that in a definition
an implication means a biconditional statement.
-
In the fifth lecture, we learned that an integer is odd if and only if it is of the form 2k+1.
We also studied equations of the form ax+by=c over the integers.
-
In the sixth lecture, we studied inequalities and backward argument.
-
In the seventh lecture, we proved that, for any integers m and n, mn is odd
if and only if m and n are odd. And using inductive reasoning conjectured that 1+3+...+(2k-1)=k2 for any positive integer k. Then
using a picture gave an informal proof. Then focused on another example to motivate the induction principle.
-
In the eighth lecture, we worked with the induction principle to give formal
proofs of the previously mentioned examples. The Sigma and Pi notation for sum and product were also introduced.
-
In the ninth lecture, we computed a recursively defined sequence using strong induction,
and proved that any integer more than one can bec written as product of primes.
-
In the tenth lecture, we defined the Fibonacci sequence,
and proved several properties of this sequence. The main tool was induction. In class, I also mentioned that the same strategy can be used
to study other (2-step )linearly recursive sequences. Here is a short supplimentary note on this.
-
In the eleventh lecture, we said what sets are; what it means to be an element of a set;
how to give a set: listing its elements, giving conditions of membership, giving a recipe to construct elements of a set; what it means
for a set A to be a subset of B.
-
In the twelfth lecture, we talked about operations of sets.
-
In the thirteenth lecture, we studied various properties of set operations,
and learned about universal and existensial quantifiers.
-
In the forteenth lecture, we further discussed quantifiers and introduced basics of game theory.
-
In the fifteenth lecture, we discussed quantifiers and limits.
-
In the sixteenth lecture, we helped a study on how to teach proofs effectively
by teaching an example which was proved by induction.
-
In the seventeenth lecture, we discussed what it means when we say a limit does not exist. Then we discussed the quantifier which
asserts there is a unique ....
-
In the eighteenth lecture, we discussed the Cartesian product of sets, and functions.
-
In the ninteenth lecture, we learned more about functions.
-
In the twentieth lecture, we learned about graphs of functions, injective,
and surjective functions.
-
In the twenty first lecture, we discussed surjective, bijective,
and invertible functions.
-
In the twenty second lecture, we discussed bijective functions
further, cardinality of sets, pigeonhole principle.
-
In the twenty third lecture, we discussed enumerable sets, Cantor's theorem: there
is no surjection from X to P(X), integer part of a real number.
-
In the twenty forth lecture, we proved division algorithm, congruences,
Euclid's theorem: there are infinitely many primes, congruence arithmetic and remainder of division by 9.
-
In the twenty fifth lecture, we helped a study on how to teach proofs effectively
by proving that there are infinitely many primes of the form 4k+3.
-
In the twenty sixth lecture, we proved that gcd(a,b) is the smallest positive integer that can be
written as an integer linear combination of a and b. Then we discussed several corollaries: a linear Diophantine equation ax+by=c has integer
solutions if and only if gcd(a,b)|c; the congruence equation ax≡ c (mod n) has a solution if and only if gcd(a,n)|c; Let p be a prime.
Then if p does not divide a, then a has an inverse modulo p, i.e. there is a' such that aa'≡ 1 (mod p); If p|ab, then either p|a or p|b.
-
In the twenty seventh lecture, we discussed Euclid's algorithm and how to find an integer
solution of a linear Diophantine equation.
|
