13 Properties of Estimators and Tests
13.1 Comparing estimators
A normal distribution is symmetry about its mean, so that its mean and median coincide. The question therefore arises: Should be use the sample mean or the sample median to estimate that parameter? Both seem equally natural, but the mean corresponds to the MLE. We can run some simulations to compare these estimators. And indeed, the sample mean is somewhat better than the sample median (in terms of mean squared error).
q = 10
n_grid = 2^(1:q) # sample sizes
B = 1e3 # replicates
mean_error = numeric(q)
median_error = numeric(q)
for (k in 1:q) {
n = n_grid[k]
mean_out = numeric(B)
median_out = numeric(B)
for (b in 1:B) {
x = rnorm(n) # normal sample
mean_out[b] = mean(x) # sample mean
median_out[b] = median(x) # sample median
}
mean_error[k] = mean(mean_out^2) # MSE for the sample mean
median_error[k] = mean(median_out^2) # MSE for the sample median
}
matplot(n_grid, cbind(mean_error, median_error), log = "xy", type = "b", lty = 1, pch = 15, lwd = 2, col = 2:3, xlab = "sample size", ylab = "(estimated) mean squared error")
legend("topright", legend = c("sample mean", "sample median"), lty = 1, pch = 15, lwd = 2, col = 2:3)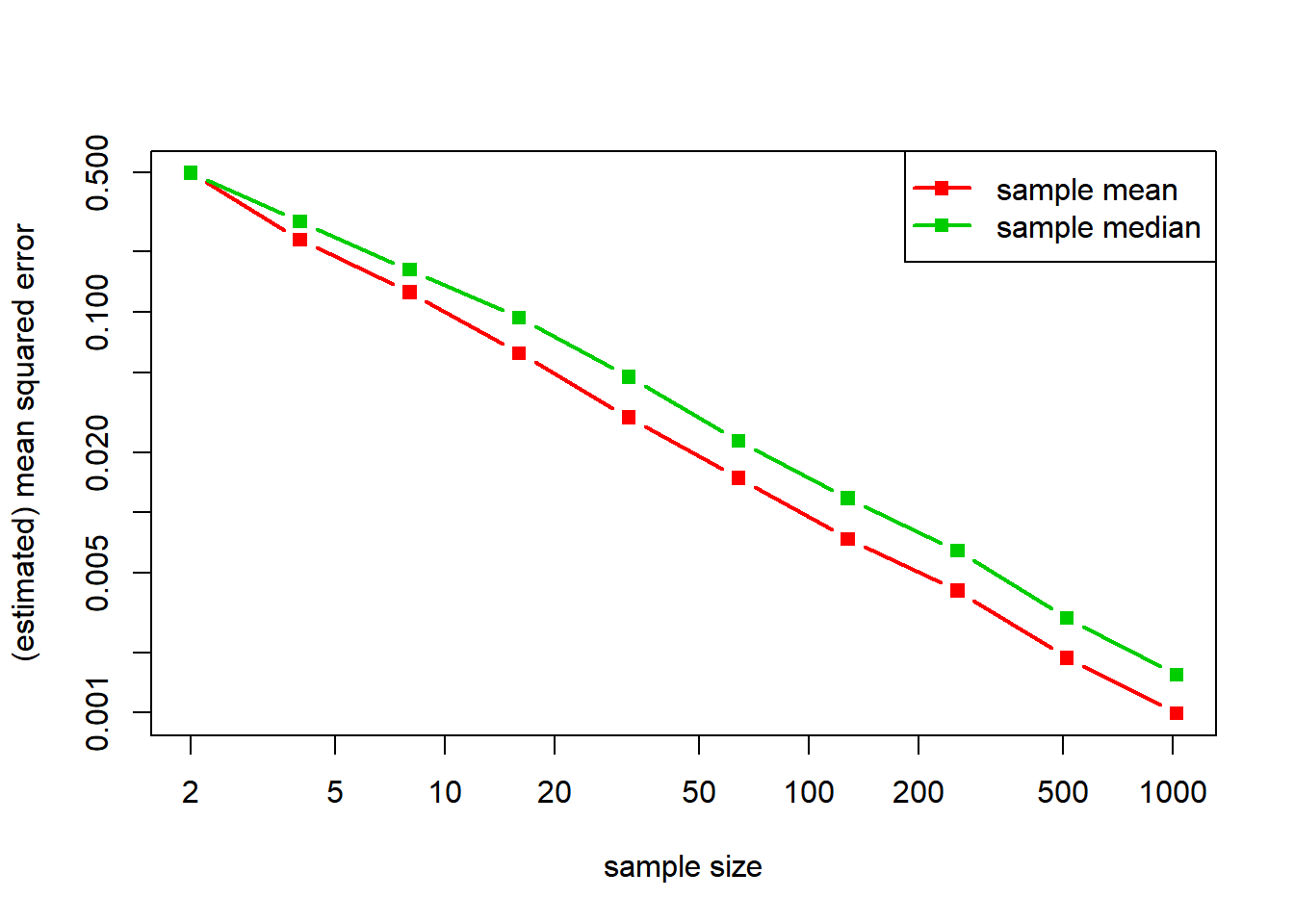
If instead of considering a normal distribution we consider a double-exponential distribution, the situation is exactly reversed.
q = 10
n_grid = 2^(1:q) # sample sizes
B = 1e3 # replicates
mean_error = numeric(q)
median_error = numeric(q)
for (k in 1:q) {
n = n_grid[k]
mean_out = numeric(B)
median_out = numeric(B)
for (b in 1:B) {
x = rexp(n)*sample(c(-1,1), n, TRUE) # sample
mean_out[b] = mean(x) # double-exponential sample mean
median_out[b] = median(x) # sample median
}
mean_error[k] = mean(mean_out^2) # MSE for the sample mean
median_error[k] = mean(median_out^2) # MSE for the sample median
}
matplot(n_grid, cbind(mean_error, median_error), log = "xy", type = "b", lty = 1, pch = 15, lwd = 2, col = 2:3, xlab = "sample size", ylab = "(estimated) mean squared error")
legend("topright", legend = c("sample mean", "sample median"), lty = 1, pch = 15, lwd = 2, col = 2:3)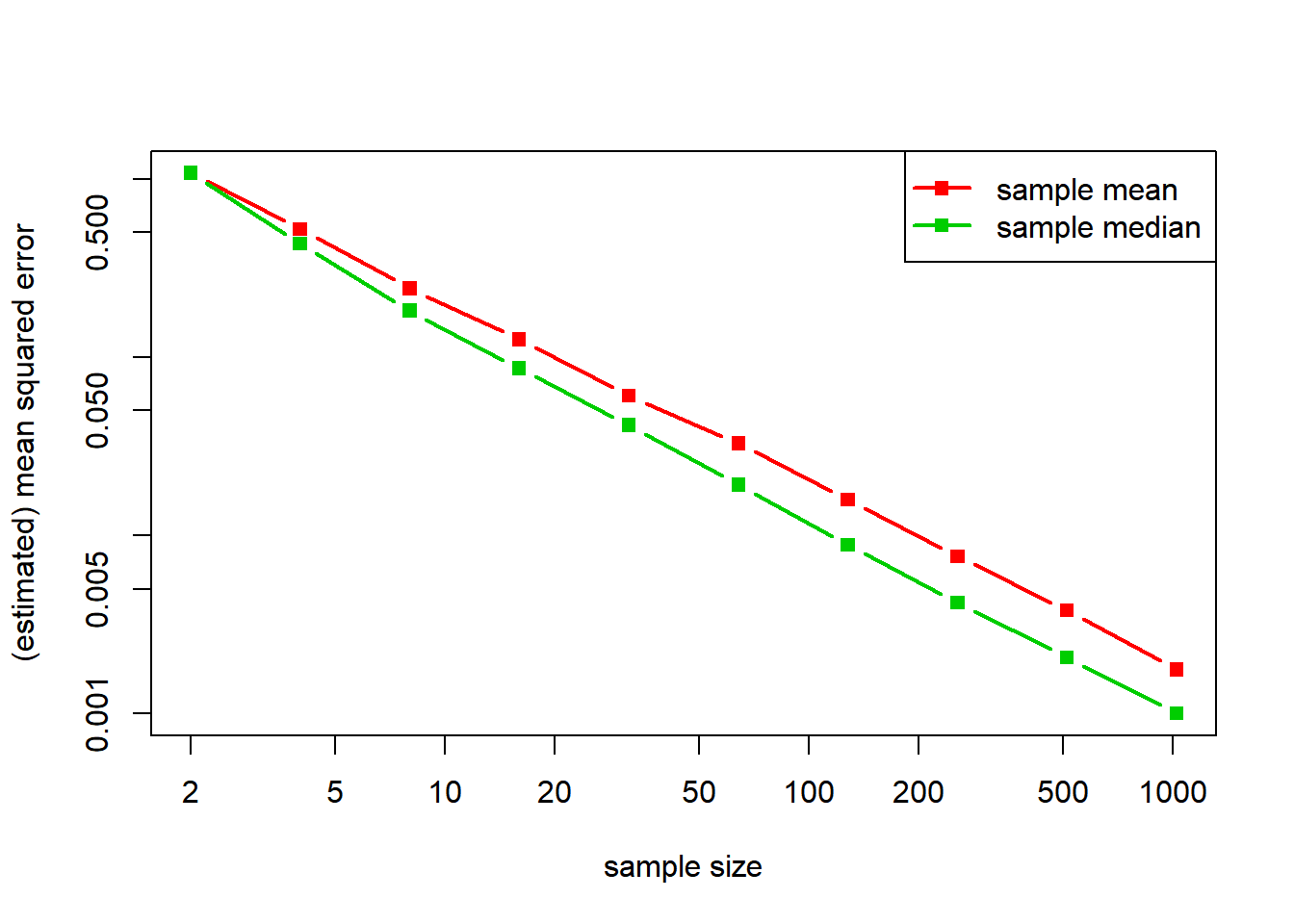
13.2 Uniformly most powerful tests
Consider testing \(Q_0\) versus \(Q_1\), two distributions on the same discrete space. The Neyman–Pearson lemma implies that any likelihood ratio test is most powerful at level equal to its size. In turn, computing a likelihood ratio test involves solving an integer program.
Q0 = runif(10)
Q0 = Q0/sum(Q0)
Q1 = runif(10)
Q1 = Q1/sum(Q1)
LR = Q1/Q0
require(lpSolve)
alpha = 0.10
Objective = Q1
Constraint = t(as.matrix(Q0))
L = lp("max", Objective, Constraint, "<=", alpha, all.bin = TRUE)
L$solution # indicator of the rejection region [1] 1 1 0 0 0 0 0 0 0 0