12 Models, Estimators, and Tests

A confidence interval, as a random interval (that is, before it is computed based on observed data) is not guarantied to contain the true value of the parameter of interest (the one the interval is built for). It only contain the true value of the parameter with some probability equal to its level. To illustrate this, we consider the Clopper–Pearson two-sided confidence interval for the parameter of a binomial. (The number of trials defining the binomial is fixed.)

n = 20 # number of trials
theta = 0.3 # probability parameter
B = 100 # number of replicates
L = numeric(B) # storing the lower bound of the interval
U = numeric(B) # storing the upper bound of the interval
X = rbinom(B, n, theta) # simulated data with each number corresponding to one replicate
for (b in 1:B){
  test = binom.test(X[b], n, conf = 0.90)
  L[b] = test$conf.int[1]
  U[b] = test$conf.int[2]
}
plot(0, 0, type = "n", xlim = c(0, 1), ylim = c(0, B), ylab = "Experiments", cex.lab = 1.5)
segments(L, 1:B, U, 1:B, col = "darkgrey")
abline(v = theta, col = "darkred") # indicates the true value of the parameter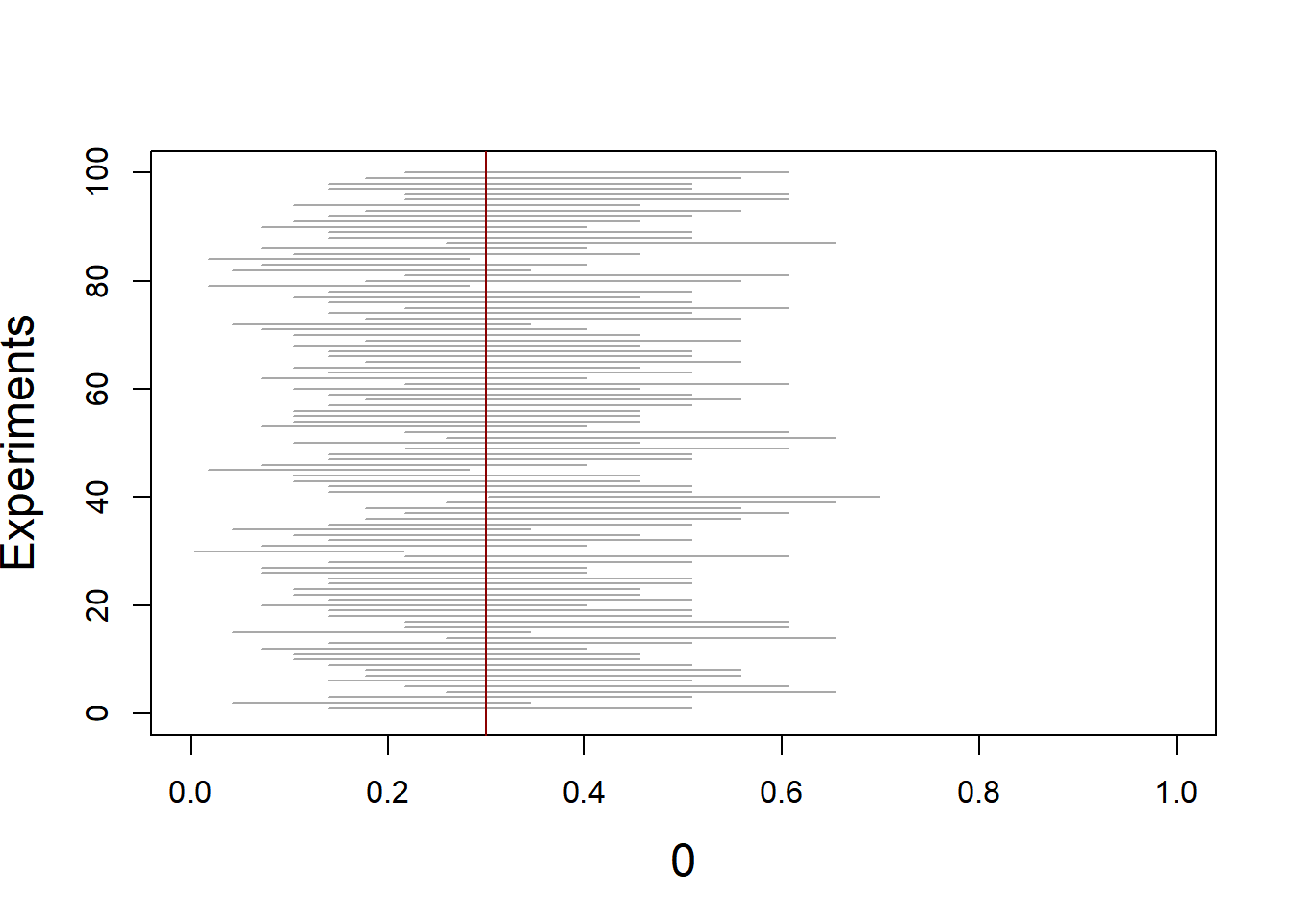

cat(paste("While the target level was 90 percent, the interval contained the true value of the parameter", sum((L < theta)*(U > theta)), "times out of", B, "replicates."))

While the target level was 90 percent, the interval contained the true value of the parameter 95 times out of 100 replicates.