17 Multiple Numerical Samples

17.1 An example of A/B testing

The modern name for two-sample comparison is “A/B testing”. This terminology is particularly prevalent in the high-tech industry. The following is an example of that and is an example that appears in Kaggle (https://www.kaggle.com/yufengsui/mobile-games-ab-testing) and DataCamp (https://www.datacamp.com/projects/184). Summarizing the description provided on Kaggle, Cookie Cats is a mobile puzzle game. As a players progress through the levels of the game, they will occasionally encounter gates that force them to wait a non-trivial amount of time or make an in-app purchase to progress. In addition to driving in-app purchases, these gates serve the important purpose of giving players an enforced break from playing the game, hopefully resulting in that the player’s enjoyment of the game being increased and prolonged. But where should the gates be placed? In the present experiment, the effects of placing the first gate at level 30 and level 40 are compared, in particular terms of player retention. Here are the variables:

userid: player identifier
version: level where the first gate appeared (for that player)
sum_gamerounds: number of game rounds played (by that player) during the first week after installation
retention_1: did the player come back and play 1 day after installing?
retention_7: did the player come back and play 7 days after installing?

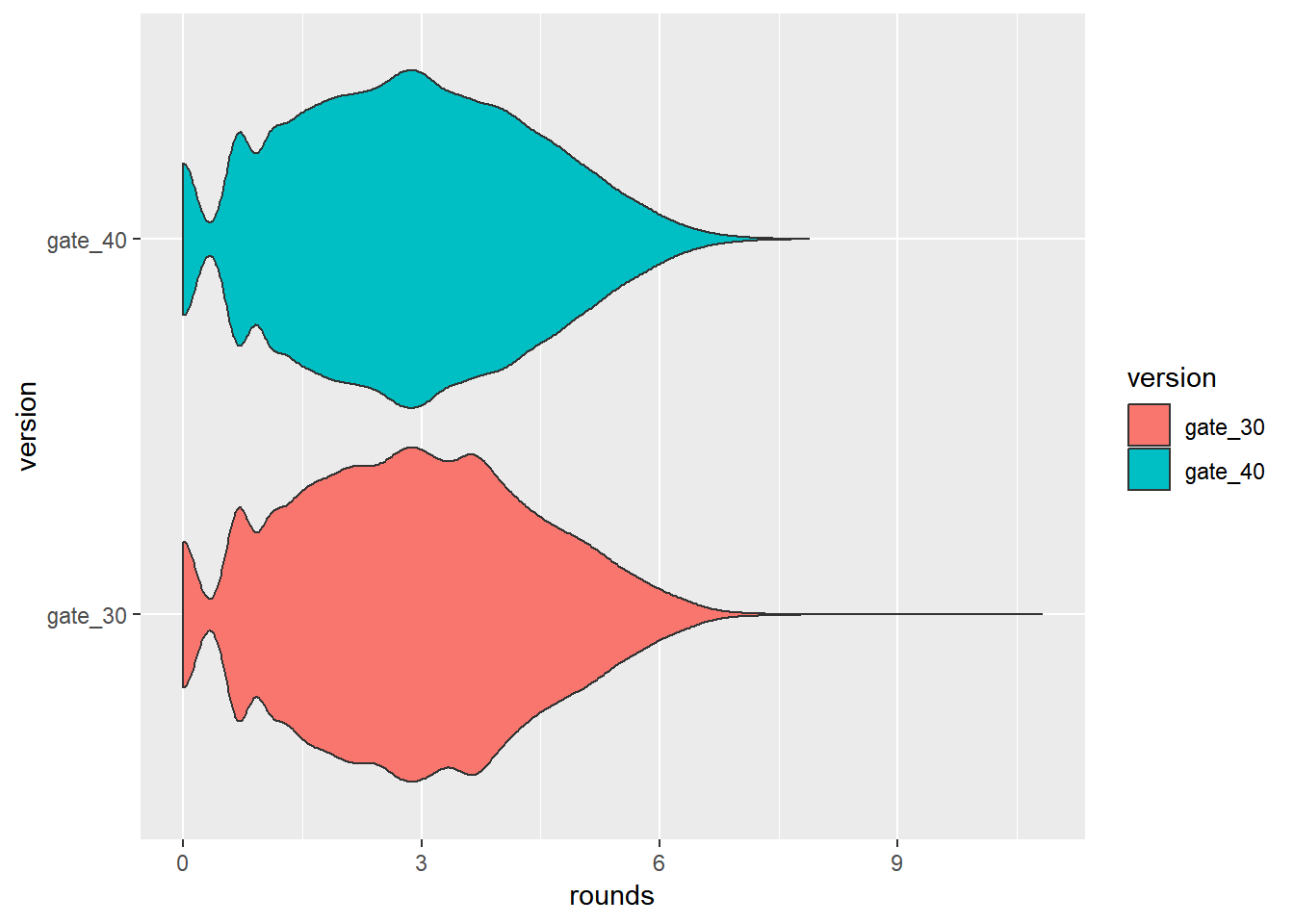
cookie_cats = read.csv("data/cookie_cats.csv")

We focus on the number of game rounds played in the first week after installation. We start with some plots.

dat = cookie_cats[, 2:3]
names(dat) = c("version", "rounds")

17.2 Plots

We first explore the data with some plots. ### Boxplots

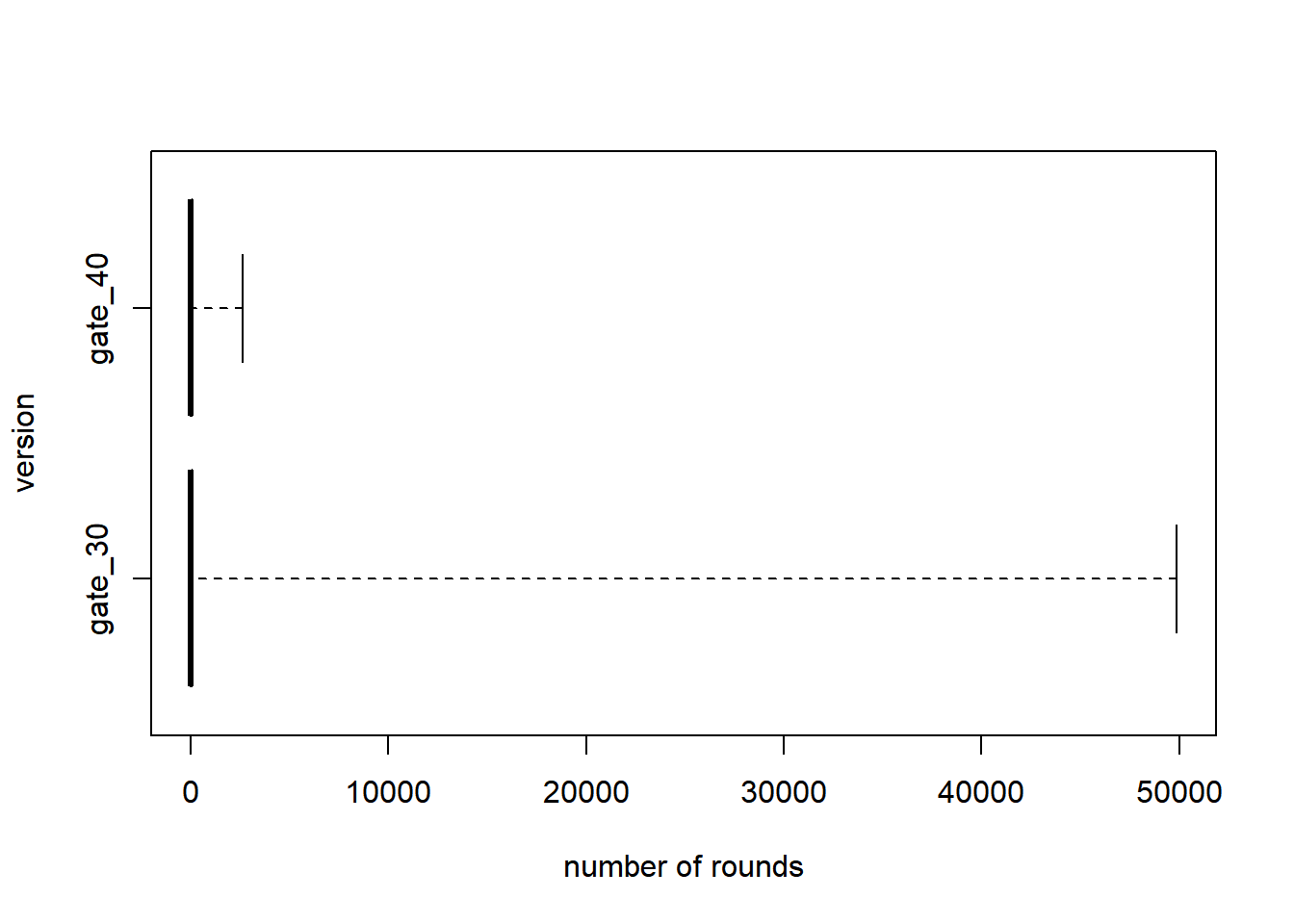
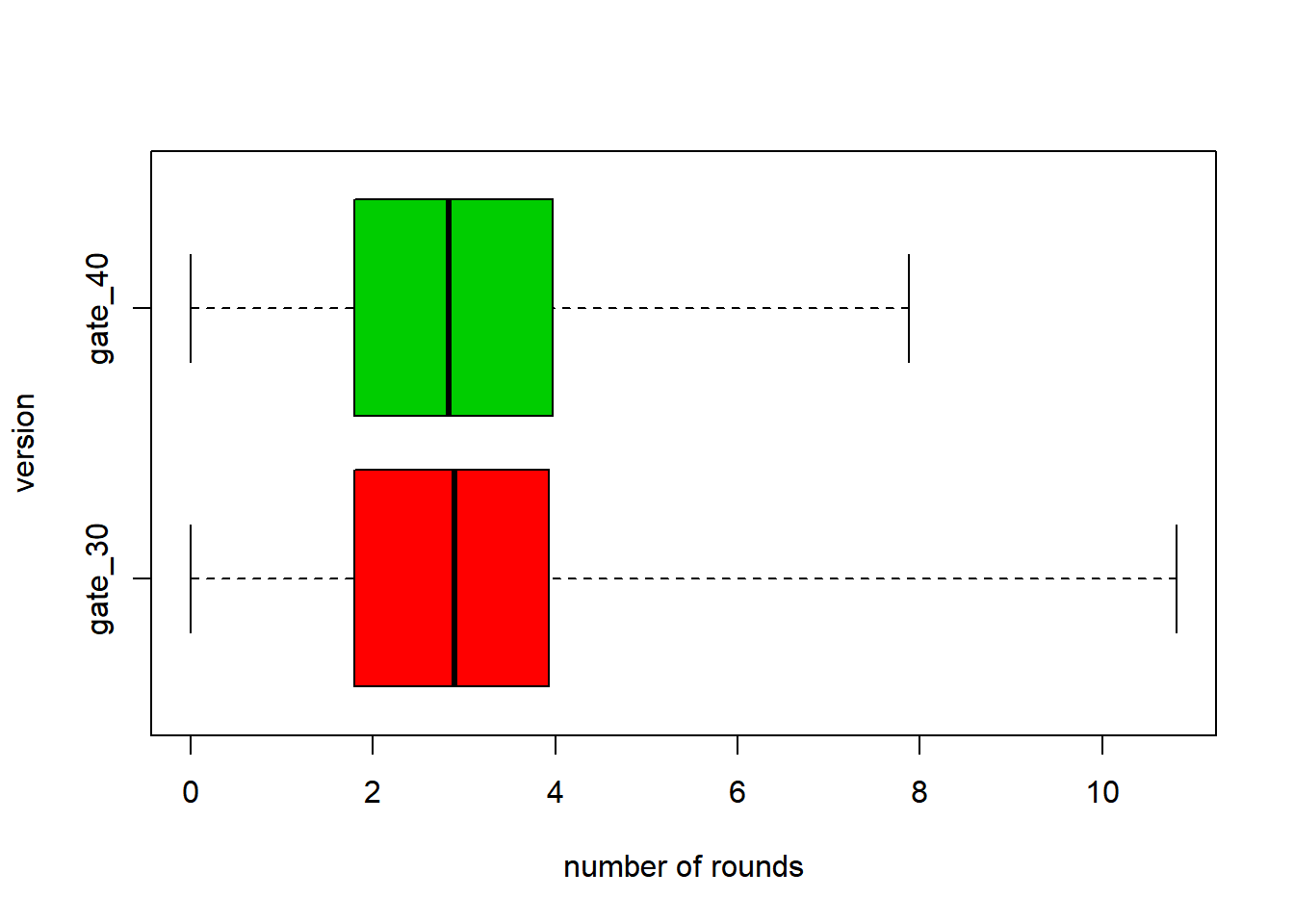
boxplot(rounds ~ version, data = dat, range = Inf, col = 2:3, horizontal = TRUE, xlab = "number of rounds", ylab = "version") # we cannot see much

boxplot(log(rounds + 1) ~ version, data = dat, range = Inf, col = 2:3, horizontal = TRUE, xlab = "number of rounds", ylab = "version") # we cannot see much

We work with a log scale henceforth.

dat$rounds = log(dat$rounds + 1)

17.2.1 Histograms

rounds_30 = with(dat, rounds[version == "gate_30"]) 
rounds_40 = with(dat, rounds[version == "gate_40"]) 
par(mfrow=c(2,1))
hist(rounds_30, main="", xlim = range(dat$rounds), xlab="", las = 1 , col = 2, breaks = 50)
hist(rounds_40, main="", xlim = range(dat$rounds), xlab="", las = 1 , col = 3, breaks = 50)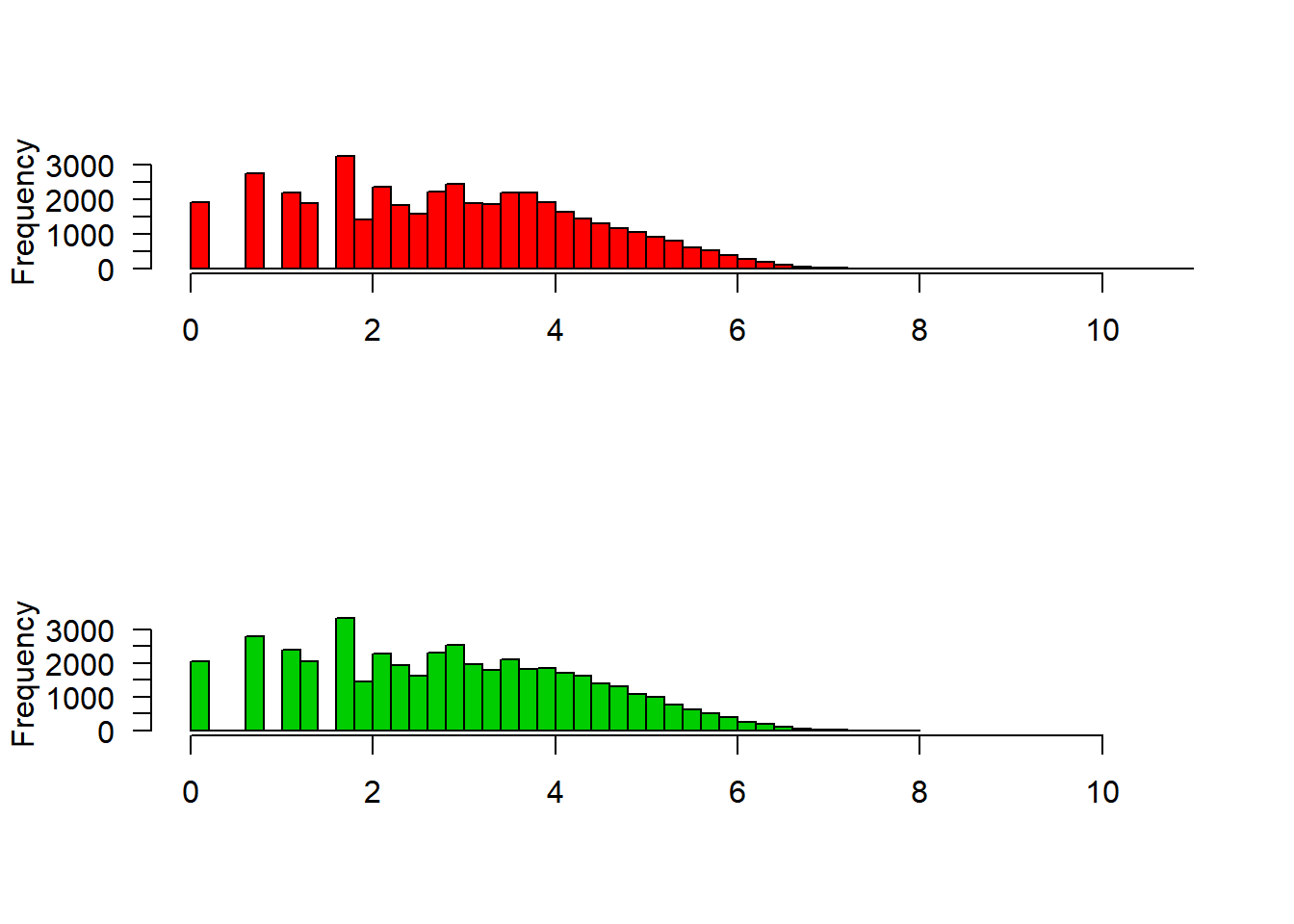

17.2.2 Violin plots

require(ggplot2)
ggplot(dat, aes(version, rounds, fill = version)) + geom_violin() + coord_flip()

17.3 Tests

We now perform some tests. ### Welch–Student test To compare the two means, we simply apply the two-sample Welch–Student test. (The samples are quite large and after the log transformation their distrbutions are not overly skewed.) The function also computes the related confidence interval.

t.test(rounds_30, rounds_40)


    Welch Two Sample t-test

data:  rounds_30 and rounds_40
t = 1.8142, df = 90177, p-value = 0.06964
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -0.001459544  0.037796681
sample estimates:
mean of x mean of y 
 2.888910  2.870742

We find that there is some evidence that with the first gate shown at level 30 a player will play more rounds (at least in the first week after installing the game). ### Rank tests We can also apply goodness-of-fit tests such as the Wilcoxon rank-sum test and the Kolmogorov–Smirnov tests. (Both are rank-based tests and therefore return the same p-value regardless of whether they are applied before or after transformation.)

wilcox.test(rounds_30, rounds_40)


    Wilcoxon rank sum test with continuity correction

data:  rounds_30 and rounds_40
W = 1024331251, p-value = 0.05021
alternative hypothesis: true location shift is not equal to 0

ks.test(rounds_30, rounds_40)


    Two-sample Kolmogorov-Smirnov test

data:  rounds_30 and rounds_40
D = 0.010271, p-value = 0.01719
alternative hypothesis: two-sided

Again, there is some evidence that the two samples do not come from the same distribution. In any case, although somewhat statistically significant, the difference may not be meaningful as it is quite small. (The median number of rounds played differs by just 1.)