Poset is short of partially ordered set. A poset of size `n` consists of a set of `n` elements together with a binary relation.
A finite poset can be represented by a Hasse diagram (directed acyclic graph). In Hasse diagrams, each vertex stands for an distinct element and each arrow is from smaller element to larger element. A linear extension of a poset of size `n` is a way to fill integers `\{1,2,\cdots,n\}` in the vertice such that all arrows are satisfied.
For example, the second P in our logo represents a poset and the number of linear extensions is `6`.
We define a family of posets `\{P_n\}`. One can easily get what `P_n` looks like based on `P_1`, `P_2`, `P_3` and `P_4`.
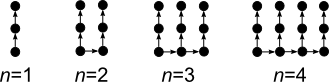
`a(n)` is the number of linear extensions of poset `P_n`. For example, `a(1)=1` and `a(2)=10`.
Find `a(n)`.