This problem is inspired by cannons in Xiangqi, a.k.a. Chinese chess.
Suppose we put $k$ cannons in a $n\times n$ board. If there are three or more than three cannons in a row or column, they can attack each other. In other words, cannons are non-attacking if there are at most $2$ cannons in each row and column.
Clearly, for a $n\times n$ board, we can put at most $2n$ non-attacking cannons.
$a(n)$ is the number of ways to place $2n$ non-attacking cannons in a $n\times n$ board.
For example, $a(2)=1$, $a(3)=6$ and the following figure is an example of placing $8$ non-attacking cannons in a $4\times 4$ board.
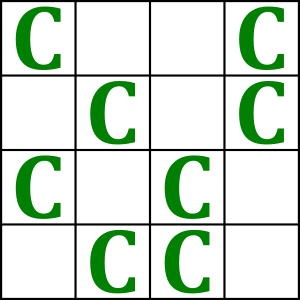
An observation is that $a(n)\le \frac{(n!)(!n)}{2}$, where $!n$ is the number of derangments of $\{1,2,\cdots,n\}$.
Find $a(n)$.