Visualizing Solutions to ODEs
In this lab, we are going to investigate differential equations of the form
| (1) | dy⁄dx = ƒ(x,y) |
using direction fields (also called slope fields). The direction field of this differential equation is a diagram in the (x,y) plane in which there is a small line segment drawn with slope ƒ(x,y) at the point (x,y). For example, the direction field of the differential equation
| (2) | dy⁄dx = x |
looks as follows:
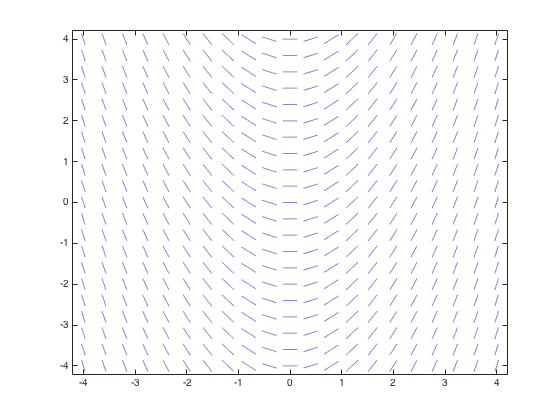
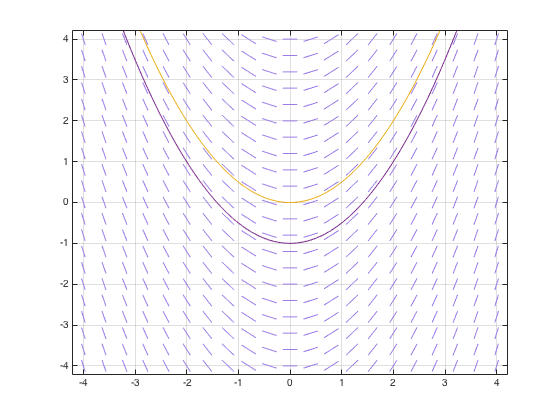
Two possible solutions (of infinitely many) to (2) are shown on the graph below. One solution passes through the point (0,0), while the other passes through the point (0,-1). Note that for each point a solution passes through, the corresponding curve below follows the same direction as the line segments around it.
The above direction fields were drawn with the help of a MATLAB M-File called slopefield.m, with which we will shortly become familiar. But first, let's think about the above direction field without the aid of a computer.
The differential equation (2) can be solved analytically, with solution
| (3) | y(x) = x2⁄ 2 + C |
where C is a constant. Notice how the direction field above confirms that (3) is the solution to the differential equation (2): if we start at any point on the graph, and we follow the lines of the direction field, we get a curve of the form given in (3). The constant C is determined by our starting point (i.e., the initial conditions).
- Sketch (by hand, without using MATLAB) the direction field of the differential equation dy⁄dx = y⁄2 for x and y values between -5 and 5. (You do not need to include this sketch in your write-up.)
- On your direction field, add a curve (by hand) that approximates the solution passing through the point x = 0, y = 1.
- Now solve the differential equation given in part (a), either working it out by hand or using the
dsolvecommand that we saw in Assignment 1. Compare your answers to parts (a) and (b).
It is apparent from the above exercises that drawing the direction fields associated to more complicated differential equations will be a tedious task. Let us now take a closer look at some convenient tools that can help us.
Drawing Direction Fields & Solutions
Before we begin, you will need to make sure you have the four M-Files slopefield.m, drawode.m, phaseplane.m, and drawphase.m installed. If you are working on an ETS machine or using the virtual lab, they should already be there. If not, you can download them all here . If this link does not work please try opening in a different tab, using a different browser, or downloading on a different device (phone/tablet). Once you've downloaded this folder, move each of the four M-Files into your working directory, which can be located at your current folder. If you can see those files in your current folder, then it's safe to use them. If you choose to use MATLAB online or MATLAB Mobile, you may upload those four M-files to your MATLAB Drive.
SLOPEFIELD
The M-File slopefield.m defines a new function, slopefield, which draws direction fields of a given first-order ordinary differential equation. If you like, you can type help slopefield into MATLAB to read the documentation for the function. We're going to work through an example to see how slopefield works.
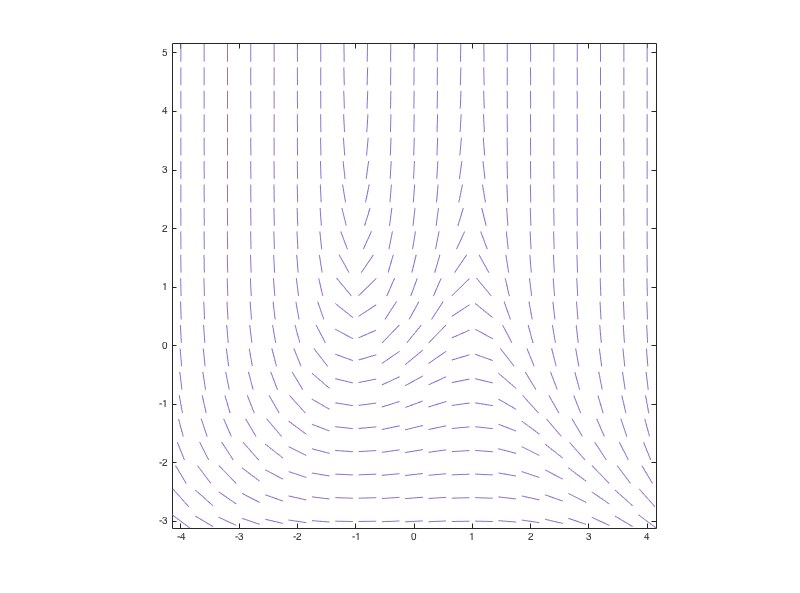
Let's try to use slopefield to draw a direction field for the differential equation
| (4) | dy⁄dt = (1 - t2) ey. |
If we check the documentation, we'll see that slopefield takes four inputs: a function, a range of values for the independent variable, a range of values for the dependent variable, and finally a number (density) that controls how many segments we'll draw on our field.
Thus, to use slopefield, we first need to define a new function (say, ƒ(t,y); the name doesn't matter) that represents the right-hand side of this ODE. Recall that we can do that by typing
f = @(t,y) (1 - t^2)*exp(y)
Suppose we'd like to see the direction field for t values between -4 and 4 and y values between -3 and 5, with about 20 marks in each direction. Then we simply need to type
>>slopefield(f, [-4,4], [-3,5], 20)
MATLAB produces the following plot:
For the remainder of this lab, we will refer to the independent variable in our differential equations as time, although the name of that variable need not be t, and the independent variable for the equations in question may not literally be time.
Now we can use MATLAB to quickly produce direction fields. Let's explore how these direction fields relate to the solutions of the ODE by learning how to plot some solutions.
DRAWODE
MATLAB includes a number of functions designed to numerically approximate solutions to ODEs. However, they are somewhat inconvenient for our purposes because they typically only compute either forwards or backwards in time, but not both. Thus, for instance, you can't call on these functions to plot the solution to dy⁄dt = (1 - t2) ey for t between -4 and 4 with the initial value y(1) = -1, because t = 1 is neither the start time nor the end time.
The M-File drawode.m rectifies this issue. It defines a new function drawode that can plot solutions to a first-order initial value problem regardless of where the "initial" time is located. In the example we just mentioned, it would be able to go backwards from t = 1 to t = -4 and also forwards from t = 1 to t = 4. Let's go ahead and use drawode to do that. Again, it may be useful to check the documentation by entering help drawode.
The function drawode takes four inputs: the function that represents dy⁄dt (which, in the case of equation (4), we already named f), a range of times, an initial time t0, and finally an initial value y0 = y(t0).
Again, we want t to be between -4 and 4, and now we'd like y(1) to be -1. So we plug all that in to the appropriate places in drawode:
drawode(f, [-4,4], 1, -1)
Now MATLAB draws this plot:
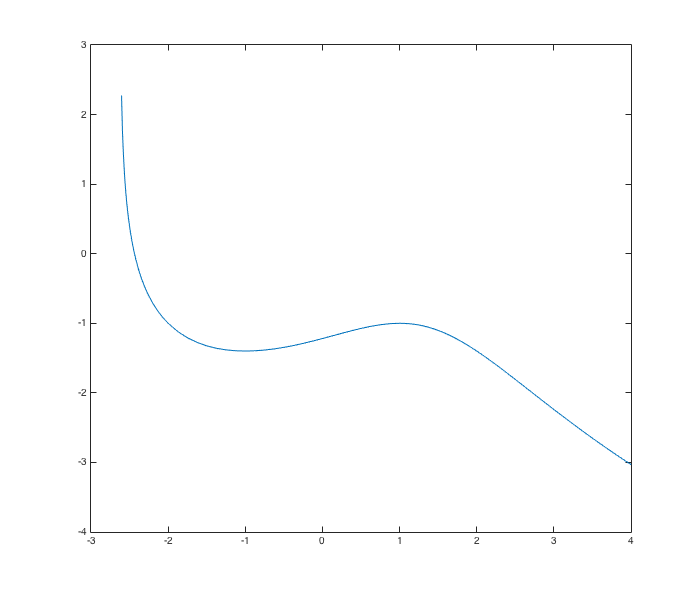
Why do you think the graph ends around t = -2.6, even though we asked it to show t values down to -4? A look at the direction field from the first example may help to explain. In fact, it would be very nice if we could look at both the direction field and our solution curve at the same time.
Combining Plots
Unfortunately, if we try to run slopefield and drawode in succession, the first plot (our direction field) disappears; MATLAB overwrites it with the new graph made by drawode. The keys to solving this are the commands hold on and hold off.
If you use MATLAB to produce a figure and then enter hold on, MATLAB will start drawing any new plots on the same figure, without erasing whatever was there before. After you're done, hold off turns off this behavior so that you can erase your work and draw new plots. Let's see this in action using the work we've already done. (Here, your up-arrow key may prove useful.)
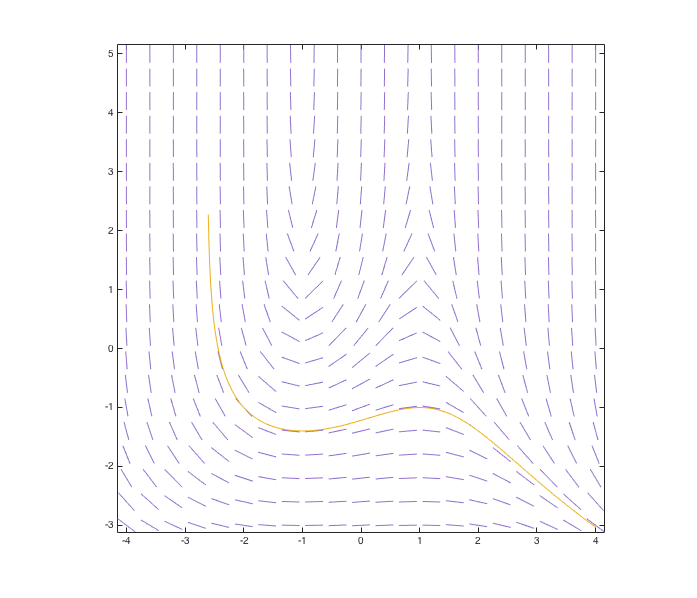
We'd like to draw a direction field for the ODE given in (4) and then plot the solution passing through (1,-1) on that direction field. In MATLAB's command prompt, we'll enter the following:
>> slopefield(f, [-4,4], [-3,5], 20)
hold on
axis([-4,4,-3,5])
drawode(f, [-4,4], 1, -1)
hold off
Finally, we get our combined plot:
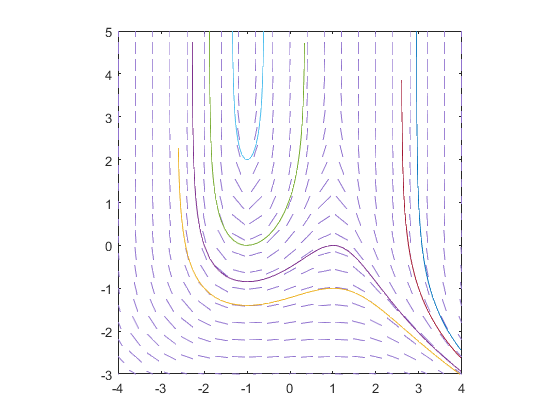
We're not limited to graphing just one solution curve, however. Let's try a few more initial values:
>> slopefield(f, [-4,4], [-3,5], 20)
hold on
axis([-4,4,-3,5])
drawode(f, [-4,4], 1, -1)
drawode(f, [-4,4], 1, 0)
drawode(f, [-4,4], -1, 0)
drawode(f, [-4,4], -1, 2)
drawode(f, [-4,4], 3, -1)
drawode(f, [-4,4], 3, 1)
hold off
You can copy and paste this code into MATLAB to try it for yourself.
Adjusting the Viewing Area
In Assignment 1, we learned that we could adjust the axes on a plot by using the menu option Edit ❯ Axes Properties…. However, this will not work with slopefield, since slopefield only draws the direction field over a limited area. To change the boundaries on the axes, we'll have to change the bounds we include in slopefield.
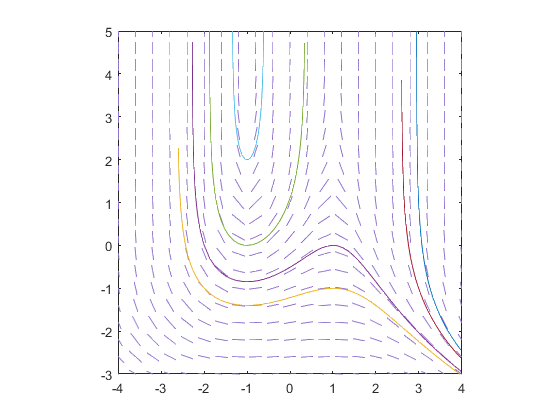
We could go through and adjust the range of t values every single time we call slopefield and drawode, but when you're drawing a lot of solution curves the way we did in Example 2.3, that can be a tedious task. Instead, if we had anticipated that we might want to zoom in or out, it would have been better from the beginning to do the following:
>> tmin = -4; tmax = 4;
slopefield(f, [tmin,tmax], [-3,5], 20)
hold on
axis([tmin,tmax,-3,5])
drawode(f, [tmin,tmax], 1, -1)
drawode(f, [tmin,tmax], 1, 0)
drawode(f, [tmin,tmax], -1, 0)
drawode(f, [tmin,tmax], -1, 2)
drawode(f, [tmin,tmax], 3, -1)
drawode(f, [tmin,tmax], 3, 1)
hold off
Now, if we simply change the value of tmin to -5, change the value of tmax to 5, and adjust the y values in slopefield as desired, we can quickly rescale the plot with all six solution curves included.
If you think you'll enjoy the challenge, you might want to devise an even more efficient way to draw a lot of solution curves, perhaps using for loops and matrices.
When looking at graphs like these, you might find it useful to try the commands grid on and grid off, which turn on and off the grid lines on the plot, respectively.
Consider the differential equation
| (5) | dy⁄dx = (cos(x) + sin(y))(1 - y). |
- Plot a direction field for (5) for x and y between -5 and 5. Use the
holdcommands anddrawodeto plot at least two solution curves on this direction field, one of which passes through the point (1,2) (that is, x = 1 and y = 2). Paste your plot into your Word document.[Hint: You may modify the bounds on the axes in the example above.]
- Considering how complicated differential equation (5) appears to be, why do you think we might want to plot a direction field?
Modeling: Newton's Law of Cooling
We'll now look at a real-world application in which direction field plots will give us valuable information about the solutions to our differential equation. Newton's law of cooling models the temperature change of an object at a certain temperature when placed in a surrounding environment of a different temperature. The law can be stated as follows:
| (8) | dy⁄dt = k(A - y) |
where y(t) is the temperature of the object in degrees Fahrenheit at time t in hours, and A and k are constants.
Plot a direction field for (8) with A = 3, k = -2, and minimum value of t is zero (since we are not interested in negative times here). You can choose an appropriate maximum value for t and minimum and maximum values for y. Include the direction field in your document.
Now plot some direction fields for other values of A, and graph a few solution curves on those direction fields using drawode by choosing some initial values. You don't need to include these plots in your document. What property do you think A represents in real life? [Hint: Think about the temperature at which the solutions stabilize.]
Let us try to figure out how long it will take to defrost a frozen chicken breast in the fridge, which keeps a constant temperature of 41°F. The chicken breast has been in the freezer for a while, so its temperature is uniform at -6°F. We'll suppose k = 0.4, based on the properties of the chicken.
- Recall that an initial value problem consists of a differential equation along with an initial condition. Write out the initial value problem that we must solve here. (We already have the differential equation, so this means you need to find the appropriate initial condition.)
- To simulate the conditions in the fridge, we must pick the parameter A. What do you think the value of A should be?
- Let us consider the chicken breast fully defrosted when the temperature reaches 39°F. How long does it take to defrost a chicken breast under the above conditions? A rough estimate from a direction field plot is sufficient. [Hint: You may need to adjust the axes on your plots.]
- How much time would be saved if the chicken breast were thawed on the kitchen counter instead, given that room temperature is around 69°F?
Systems of ODEs
So far we have examined differential equations of the form
dx(t)⁄dt = f(x(t)).
For example, if f(x) = 2x + 3, then this equation says x′(t) = 2x(t) + 3. A system of differential equations involves several equations that tie together one or more variables. For example, a 3×3 system of first-order differential equations
dx(t)⁄dt = f1(x(t), y(t), z(t))
dy(t)⁄dt = f2(x(t), y(t), z(t))
dz(t)⁄dt = f3(x(t), y(t), z(t))
constrains the functions x(t), y(t), z(t). A specific example is given by:
| (9) |
dx(t)⁄dt = 2x(t) + 3y(t) - 4z(t) dy(t)⁄dt = -3x(t) - y(t) + 2z(t) dz(t)⁄dt = x(t) + y(t) - z(t) |
Here, f1(x, y, z) = 2x + 3y - 4z, f2(x, y, z) = -3x - y +2z, and f3(x, y, z) = x + y - z.
Mathematical models like Newton's laws produce systems like these, and the initial conditions (x(0), y(0), z(0)) = (x0, y0, z0) are determined by whatever data you measure at t = 0. Systems with hundreds of equations or more are commonplace in engineering, biochemistry, and most types of technology. One major conceptual point is that such a system produces a direction field (in this case in three dimensions). Then the solutions can be seen as curves, with very similar properties to what you saw with slopefield for 2×2 systems. The course has not yet covered systems of equations, but don't worry! Our goal in these labs is to give you a taste of what a system of differential equations is, a few examples, and an idea where the course is going. These labs will discuss everything you need in order to grasp this.
A system with hundreds of equations can be difficult to understand and impossible to visualize. The way to understand large systems is to get a good understanding of systems of two or three equations, both graphically and algebraically. In systems of hundreds of variables, the algebra is very similar to the smaller systems, and even though we can no longer view our system graphically, examining solutions visually in lower dimensional systems provides us with an intuition that applies to the larger system. The next few sections will help to familiarize you with the basic definitions and ideas of two-dimensional systems, which will prepare you for when systems are covered more thoroughly in Assignment 4.
A two-dimensional first-order system is a pair of differential equations of the form
dx(t)⁄dt = f1(x(t), y(t))
dy(t)⁄dt = f2(x(t), y(t))
with an initial condition (x(0), y(0)) = (x0, y0). Under conditions on f1 and f2 (namely, that each is continuous and differentiable), specifying (x0, y0) determines the solutions (x(t), y(t)) uniquely—that is, there can be no other functions (x(t), y(t)) that satisfy both differential equations and also satisfy the initial conditions (x(0), (0)) = (x0, y0).
An excellent way to think of a system of ODEs is in terms of the left-hand side giving a tangent vector and the right side giving a vector field. To be more precise, to each point (x, y), associate a 2-vector
(f1(x,y), f2(x,y)).
This captures all the information in the right side of the ODE. To understand the left side of the ODE, recall from Math 20C that a curve C parametrized by (x(t), y(t)) has derivative (x′(t), y′(t)) pointing tangent to C. Putting these two facts together, we can deduce that a solution curve to the ODE must at each point (x, y) have the vector (f1(x,y), f2(x,y)) tangent to it. Different initial conditions (x0, y0) produce different solution curves.
Since a vector has both a magnitude and a direction, it can be represented visually in two dimensions by an arrow. Thus we can "draw" the vector field (f1(x,y), f2(x,y)) and look at curves tangent to it, which indeed are trajectories of solutions to our system of ODEs. This is much like what we did with slopefield, although slopefield ignored the magnitude of vectors. Our next objective is to put these ideas into action.
Drawing Phase Portraits
Double-check that your working directory contains the M-Files phaseplane.m and drawphase.m. If you are working on an ETS machine, they should already be installed; otherwise, you can download them using this link.
For a given system of first-order differential equations and a given point on the plane, there is at most one solution to that differential equation that passes through that point. When we draw a phase plane (or phase portrait), what we are doing is picking a sample of points on the plane and then, for each point, plotting the vector tangent to the solution curve that goes through that point. (This is analogous to the one-dimensional phase diagrams that you may have already seen in lecture; in those diagrams, we only drew our arrows up and down.) For our two-dimensional case, the resulting plot of vectors helps us to visualize how different solution curves behave. We'll use the command phaseplane to see some examples.
PHASEPLANE
The function phaseplane plots the phase plane at time zero for a two-equation system of first-order ODEs Y′ = g(t,Y), where t is the independent variable and Y is a 2×1 vector containing our dependent variables. In MATLAB, we write such a vector as [y1; y2]. Let's see how to use phaseplane with an example.
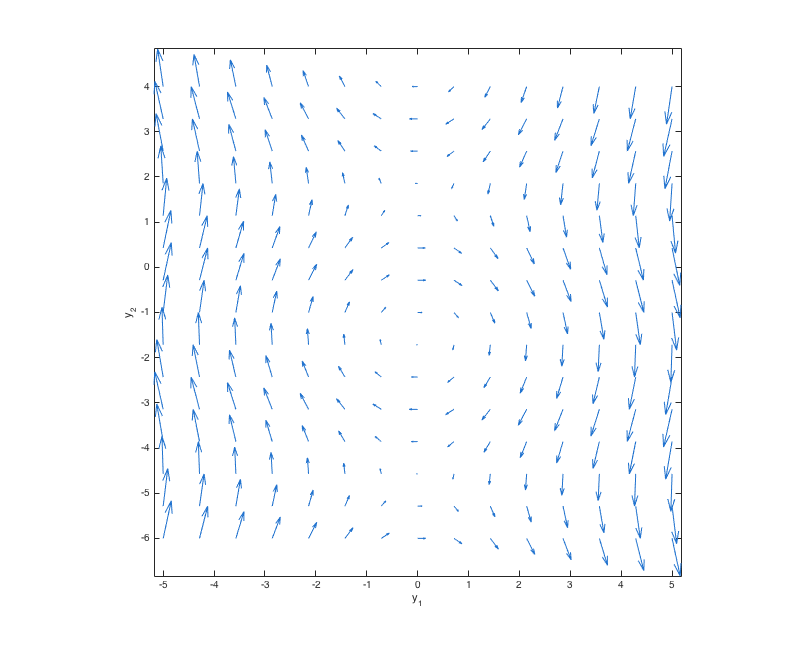
We'll use phaseplane to draw a phase plane for the system
| (10) |
dy1(t)⁄dt = cos(y2) dy2(t)⁄dt = -y1 |
We can think of a system like this in terms of vectors. Let Y be the 2×1 vector with entries y1 and y2 (our two dependent variables). Then we can write this system as
where g is a function that spits out the 2×1 vector with entries cos(y2) and -y1 (from the right-hand side of our system).
The syntax for phaseplane is very much like that for slopefield. The command phaseplane takes four inputs: the vector-valued function g(t,Y) that defines the right-hand side; a range of values for the first dependent variable y1; a range of values for the second dependent variable y2; and finally the number of vectors we want to draw in each direction on our field.
We need to define a vector-valued function, which we haven't yet learned how to do. The procedure is much like the one for real-valued functions that we've used previously. In this case, we want to enter
>>g = @(t,Y) [cos(Y(2)); -Y(1)]
Here, Y(2) represents the second element of the vector variable Y; for this system, that's our second dependent variable, y2. Of course, Y(1) is the first element of Y and stands in for y1. You can do this kind of thing in general in MATLAB: given a vector X = [x1; x2; x3; ...; xn], then X(i) returns the ith element.
Suppose we want to draw the phase plane for our system with y1 between -5 and 5 and y2 between -6 and 4, with a 15×15 grid of arrows. Then we must enter the following:
>>phaseplane(g, [-5,5], [-6,4], 15)
MATLAB will draw the plot shown below.
We'd now like to see how individual solutions to our system of ODEs appear on our phase plot. We can't graph the solutions themselves, but we can graph their projections onto the plane (their phase paths). Let's see how to do that now.
DRAWPHASE
The command drawphase defined by drawphase.m plots the projections of solutions onto our vector field, helping us to see exactly how the solutions behave. Let's use it on our system (10) of ODEs.
The syntax for drawphase is as follows:
drawphase(g, tmax, y1start, y2start)
In this command, g is the same function g(t,Y) we defined earlier. We always start at time t = 0, but tmax specifies the time at which we'd like to stop. Lastly, y1start and y2start give initial values for y1 and y2, respectively, at time t = 0.
Suppose we want to plot the solution curve that starts at y1 = 1, y2 = -3, from time zero to time 50. But remember: we want to draw this on the phase plane we've already made, without erasing the previous plot. Therefore, we need to use hold on. We should enter that like so:
>> hold on
drawphase(g, 50, 1, -3)
hold off
Or, if we were starting from scratch, we would enter
>> g = @(t,Y) [cos(Y(2)); -Y(1)];
phaseplane(g, [-5,5], [-6,4], 15)
hold on
drawphase(g, 50, 1, -3)
hold off
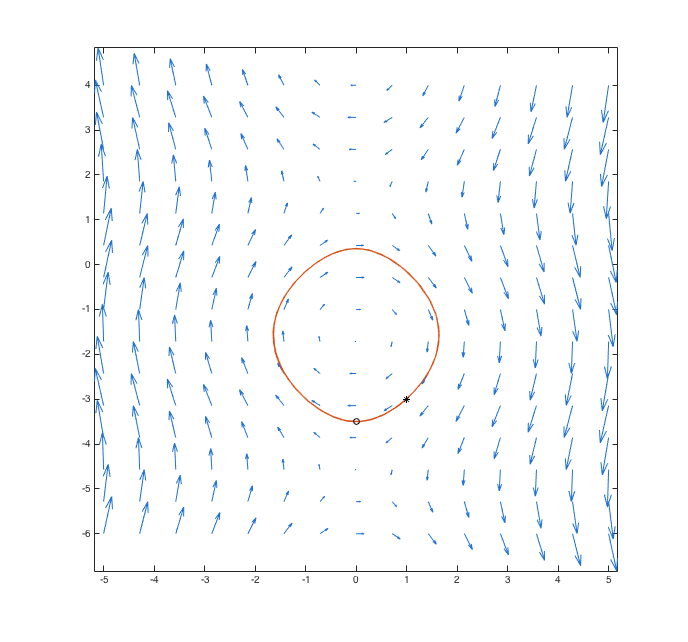
The starting point for our curve is marked with an asterisk (*), and the ending point (at whichever t value we put in for tmax) is marked with a circle.
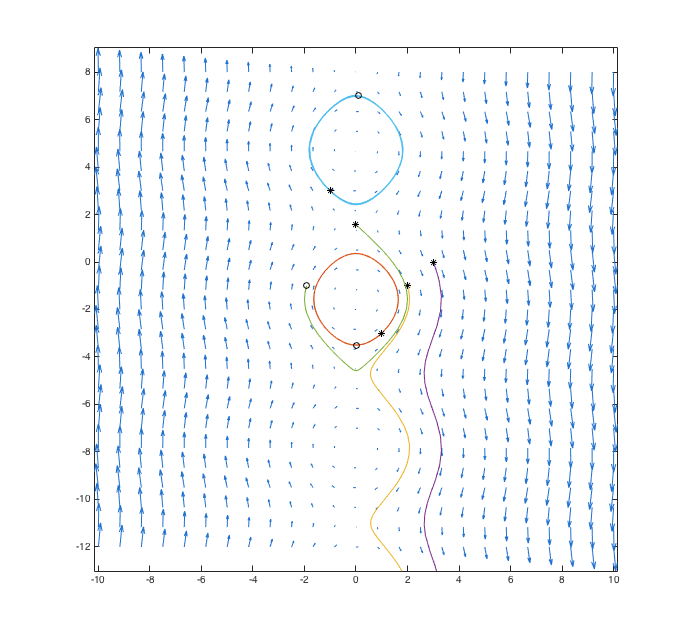
If we want, we can plot several more phase paths, adjust the viewing area, and define a variable so that it's easy to adjust our final time, just as we did before with drawode:
>>
g = @(t,Y) [cos(Y(2)); -Y(1)];
tmax = 50;
phaseplane(g, [-5,5], [-5,5], 25)
hold on
drawphase(g, tmax, 1, -3)
drawphase(g, tmax, 2, -1)
drawphase(g, tmax, 3, 0)
drawphase(g, tmax, 0, pi/2)
drawphase(g, tmax, -1, 3)
hold off
Again, it may be helpful to copy and paste this code, rather than re-typing all of it yourself.
It's time for you to draw some phase portraits on your own. Consider the 2×2 system
| (11) |
dx⁄dt = -3 dy⁄dt = 2 |
Notice that in this problem, our dependent variables are named x and y rather than y1 and y2. That's okay! The names of the variables don't actually matter. Like the function g in Example 2.4, we'll have to define a new function in MATLAB to represent the system. This time, Y(1) will stand for x, since that's our first dependent variable; Y(2) will be y.
Before we try to use MATLAB to solve this system, notice that we can solve this system easily by hand: we get x = -3t + C1 and y = 2t + C2. These are parametric equations of a straight line.
Use the techniques we've learned involving phaseplane to plot a phase portrait of (11), where the x and y values are between -5 and 5. Then, on the same plot, use drawphase to draw at least three different solution curves. Include the resulting plot in your Word document.
Now, try changing the values of x′ and y′ from -3 and 2 to other constant values. Describe in your Word document how this changes the phase portrait.
Next, let's consider the 2×2 system
| (12) |
dx⁄dt = y dy⁄dt = -x |
This problem is again fairly easy to solve by hand. Whenever we first try out a program, it's a good idea to try some problems for which you already know the answer; that way you can check that the program behaves the way you expect. In this case, by dividing the two equations, we get dy⁄dx = (dy⁄dt)⁄(dx⁄dt) = -x⁄y. Now we have a separable ODE:
y dy = -x dx.
When we integrate both sides, we find that the solution curves should look like x2 + y2 = R, where R is a constant. What kind of curve is this?
Use phaseplane to plot a phase portrait of (12), where the x and y values are between -10 and 10. [Remember that when you're defining your function g(t,Y), you need to use Y(1) to represent your first dependent variable and Y(2) for the second one.] Then, on the same plot, use drawphase to draw at least three different solution curves. Include the resulting plot in your Word document.
There is an important connection between direction fields and phase portraits.
Use slopefield to draw a direction field for the differential equation
y′ = cos(x) + sin(y),
and then draw some solution curves on the resulting direction field using drawode. Include your figure in your Word document.
Now consider the system
| (13) |
dx⁄dt = 1 dy⁄dt = cos(x) + sin(y) |
where x(0) = 0.
Tell MATLAB to create a new figure using the figure command. Then use phaseplane to draw a phase portrait for the system (13), and plot a phase path on your diagram using drawphase; the y1start value represents x(0) and should therefore be zero, while the y2start value can be any initial value for y(0) of your choosing. Finally, try adding a few more phase paths using other values for y(0). Paste the resulting figure into your Word document.
What's the relationship between your phase portrait figures and your direction field figure? [Hint: When you drew the solutions on your direction field, you should have picked several different starting values for x and y. Try drawing some phase paths on your phase portrait with the same initial values. Do the resulting curves match up?]
We'll explore this idea more in Assignment 4.
Modeling: Predator–Prey Systems
We'll now consider a mathematical model of population dynamics: a predator and prey system. Suppose that two species of animals, say, foxes and rabbits, coexist on an island. The foxes eat rabbits, and the rabbits eat vegetation, which we'll say is available in unlimited amounts. The following system of ODEs, which is called the Lotka–Volterra model, can be used to model this situation.
| (14) |
dx⁄dt = x(a - by) dy⁄dt = cy(x - d) |
Here, x is the population of rabbits, y is the population of foxes, and a, b, c, and d are positive constants. We will now use phaseplane and drawphase to investigate the solutions to this system.
- Use MATLAB to produce a phase plane of the system (14) above, with the parameter values a = 3, b = 1, c = 2, d = 3. Set the minimum values of x and y to -1 and the maximum values to 10. Where in the x-y plane are the physically possible solutions? (Remember, x and y represent populations. Can they become negative?)
- On your phase plane, use
drawphaseto plot three solution curves in the first quadrant from time zero to time 25. (i.e.,tmax=25.) Note that because of rounding error,drawphasemight fail to close a loop exactly. Include the graph in your Word document. - The predator–prey system has the following states:
- The populations of foxes and rabbits are both relatively small.
- The small number of foxes allows the rabbit population to increase.
- The increased number of rabbits allows the number of foxes to increase.
- The decreased supply of rabbits causes the fox population to decrease, returning to state A.
Conclusion
In this lab, we have seen that plots of direction fields and vector fields can be useful when trying to understand the behavior of solutions of ordinary differential equations. This is particularly important when we cannot solve the equation analytically. We have also seen how useful some relatively simple MATLAB M-Files can be in generating direction fields and plots of solutions. It is important to understand that these techniques do not in any obvious way scale to systems of hundreds of equations. Assignment 4 will present techniques which are effective for large linear systems and as such are a mainstay of modern technology and science.
Hopefully, many of you are curious. How are those solution trajectories we just saw produced? Behind the scenes, the M-Files we used in this lab work by (approximately) solving ODEs via numerical approximation. You can actually open the M-Files and read them yourself, if you want to see what they're doing. These numerical methods will be the topic of Assignment 3. They typically work well for large systems.
Last Modified: Jun 22, 2024