Knot Theory (190), Winter 2019
Justin Roberts, MWF 10-10.50 in Center 217A

The TA is Tom Grubb (tgrubb@ucsd.edu). Sections are at 6pm on Fridays in AP&M 2301. Tom's office hours are Thursdays 2-4pm in AP&M 6436.

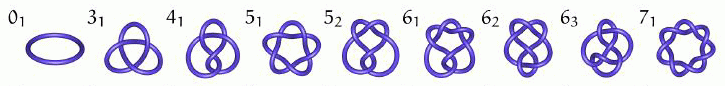
My office hours are  Wednesday and Friday 11-12 (right after class) in AP&M 7210.

Homeworks will normally be due on the Monday following the section at 4pm. There's a dropbox in the AP&M basement. Midterm will be in class on Friday Feb 8. Final is on Friday March 22nd at 8am in ****.

Grading will be 30% homework, 20% midterm, 50% final.


Knot theory

A closed loop of string in 3-space is called a knot. If it can be untangled (no cheating with scissors) into a planar circle it is called the unknot. The picture below shows the first few knots, in order of number of crossings; it starts with the unknot, then the trefoil and figure-eight:

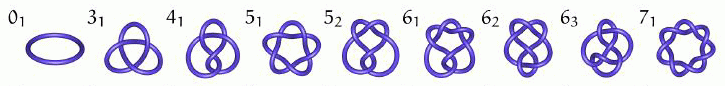
To prove this we need to apply some algebraic topology (e.g. the fundamental group of the complement of the knot in space), geometric topology (e.g. looking at surfaces associated to the knot - we will spend some time on the topological classification of surfaces in its own right), combinatorial topology (e.g. counting 3-colourings of a diagram, or the famous Jones polynomial) or other cleverness. The study of knots is both a testbed in which to apply the abstract theory of topology, and a source of new problems and methods. Plus of course it's fun! (Challenge: make a trefoil as above, and then make one where all the overcrossings go under and vice versa. Are they the same?) 

Books

My intention is to use primarily my own "knotes". (If you find typos, mistakes or things which are confusing, please let me know, as I want to try to "finish" them this term!)  

But here are some comments on other available references you might find interesting. I've put these in order of "level of mathematical sophistication" - easiest first.

C. Adams, The Knot Book (1994, W. H. Freeman) This book is a survey of knot theory. It isn't a typical textbook - it is not very detailed mathematically, since it's actually aimed at clever high-school students! But it does attempt to give the flavour of some really quite advanced topics, including current research and open problems!

M. Armstrong, Basic Topology (1983, Springer-Verlag). This is a nice undergrad-level book which teaches point-set topology and the foundations of algebraic topology. It's not directly relevant to the course, but if you are interested in point-set topology, this is probably the best place to look.

N. Gilbert and T.Porter, Knots and Surfaces (1994, OUP) An undergrad-level book, which as I remember contains some basic point-set topology too. Its focus is extremely algebraic, however - it goes into group-theoretic aspects in a lot of detail.

A. Sossinsky, Knots, (2004, Harvard). This is a translation of a French edition, "Noeuds". It is quite idiosyncratic, and has a lot of typos and mistakes, so I don't much recommend it. However, you simply must check out the awesome picture of a particular type of eel which knots itself in order to stay slippery!

C. Livingston, Knot Theory (1993, Carus Mathematical Monographs) A nice small book which surveys knot theory, again without pedantic detail, but from a perspective of someone who knows point-set topology and basic algebraic topology. So it's more a grad-level book, but it's very nicely written and perhaps still useful.

V. Manturov, Knot Theory, (2004, CRC) This book is quite new, and contains the most up-to-date results of any of the books listed here. I haven't done more than skim it myself though. I think it's a grad-level book really.

D. Rolfsen, Knots and Links (1976, Publish or Perish) The "old testament" of knot theory, with a picture on every page. It is a serious graduate-level book and it relegates a lot of proofs to exercises, but it is a unique and classic book, which you might simply enjoy paging through. (It was written before the Jones polynomial was discovered.)

W. B. R. Lickorish, An Introduction to Knot Theory (1997, Springer GTM) The "new testament" of knot theory, a graduate-level textbook dealing especially with post-Jones-polynomial knot theory. It's by my PhD advisor - you might enjoy his dry wit!

Websites

There are lots of knot theory resources on the web these days - these are the main ones that spring to mind. You'll learn a lot just by surfing these sites, and they also provide tables of calculations of pretty much every knot invariant you can think of, some software for drawing and calculating with knots, and beautiful images.

The Knot Atlas (wiki)

The KnotPlot Site

Table of Knot Invariants


Pre-requisites, and comments about 190 and 191 courses

To be honest, you don't need to know much to get started in this course! The most important thing is to be happy with linear algebra (e.g. Gaussian elimination), as we will use matrices occasionally. If you know anything about groups that might also help later on (though it depends how far we get).

The traditional first course in topology deals with ``point-set topology'': the study of metric and topological spaces, continuity, compactness, connectedness, and other properties beginning with ``c''.

This branch of the subject is really just a part of analysis, and while it is important for the foundations of the subject and can help you learn to write proofs properly, it can all seem very abstract and dry. Where are the doughnuts, coffee cups, pretzels, rubber sheets, knots and so on of popular topology?

Traditionally, we teach the more geometric, visual side of the subject after teaching all the basic tools. This is not unreasonable, but it does take a long time to do properly, and is quite hard to motivate because it turns history on its head. After all, people have been using and thinking about knots for thousands of years, but the definition of a topological space is only a hundred years old.

Fortunately it isn't necessary to work this way round. With a little care we can do quite a lot of knot theory without needing to talk about the foundational aspects of topology.

The follow on Math 191 course will be more of a "traditional" algebraic topology course.


Homework problems

One of the common problems faced by students in topology is deciding how much detail to write in proofs; the subject spans a great range, from the most pedantic and precise point-set arguments, to visual arguments which can seem like ``hand-waving''. I hope that the course will help you in general to appreciate and produce ``good mathematics'' at whatever level is appropriate.

You may find the homework questions a bit strange to start with... DON'T PANIC! Here are a few comments.

1. They are not like calculus problems, where you just manipulate formulae and write "equals, equals, equals" down the left-hand side of the page! The idea is generally to prove things.

2. A proof will often amount to just presenting a logical argument or explanation in English. Don't be afraid to write plenty of words - just make sure that they are clear meaningful words, and not waffle! You may feel that a verbal argument isn't really mathematical, but this is not true: maths is about the precise communication of precise ideas, and they don't always need to contain formulae and funny symbols.

3. Please try to write coherently! One helpful tip is to keep a particular reader in mind: imagine that you are trying to convince a fellow member of the class that something is true, and that they will not necessarily `know what you mean' if you write unclear, vague and confusing things, and will argue with you if there are gaps in what you say.

4. In a high-level subject like topology, you often have to use a bit of judgment to decide how much detail to put into your argument; this comes mostly with experience. If, for example, you find you need to appeal to some `obvious' fact,first ask yourself whether it really is obvious! Are you confident that you could prove it if challenged? If so, it's probably OK to just say that you are using it, and not bother writing its proof. But if you have no idea at all how to prove it, then it may well in fact not be true, and you should be wary! (If you can't see any way of doing without the `fact', you can start off by saying "Assuming it is true that..."; that way,your proof will still be true, even if the hypothesis you need isn't!)

5. The homework questions are very variable in nature. Some are easy; some are hard; some are much longer than others; some are vague and open-ended... they are meant to make you think and learn, and not to represent what will be on exams, so don't panic! Just write down what you can However,the ones starting with something like (2005F) or (2003M) are Final or Midterm questions from that year's course; these ones are much more down-to-earth and consistent in difficulty, and they do accurately represent what exam questions are like.


Homework 1, due Tuesday 22nd Jan

Read through section 1 of the "knotes" and do exercises 1.2.6, 1.2.9, 1.2.10, 1.4.3, 1.6.2, 1.6.3, 1.6.7,  1.7.1, 1.7.2. (This first homework consists almost entirely of "problems to make you think", rather than "this will be on the exam"-type problems, so don't panic, treat it as an exercise in playing around as an important part of mathematical research!)

Homework 2, due Monday Jan 29

3.3.6, 3.3.7, 3.3.9, 3.3.10, 3.3.11, 3.3.23.

Homework 3, due Monday Feb 4

2.3.10, 3.1.5, 3.1.6, 3.1.7, 3.1.8, 3.1.9, 3.1.10, 3.2.8, 3.2.12, 3.3.21

Homework 4, due Monday Feb 11

3.3.22, 3.3.23, 3.3.24, 3.4.7, 3.4.8, 3.4.10, 4.1.7, 4.1.8, 4.1.9

MIDTERM this Friday Feb 8 in class! Please bring a blue book! It'll cover everything up to and including p-colourings. (The Alexander polynomial stuff is not included, and neither is the Kauffman bracket.) There are lots of multiple-choice questions in section 3.6 for general revision. The midterm will have some of these as well as some questions similar to down-to-earth problems in the notes. There won't be any weird questions like the ones on the first HW!

Homework 5

4.1.10, 4.1.11, 4.1.12, 4.4.5, 4.4.6, 4.5.4, 4.5.5, 4.5.6

Homework 6

4.5.3, 4.5.7, 4.6.5, 4.6.7, 4.7.1; then read section 4.9 and do 4.9.4, 4.9.5, 4.9.6, 4.9.9 (the techniques are no different from the ones used with the Jones polynomial).

Oops! Problem 4.9.6 needs to be rewritten: basically it ought to say "l=1" (not "x=1"), but even that is not quite right because of poor sign choices I made in defining the (l,m) form of the polynomial in theorem 4.9.2. The correct Conway skein relation is the thing you get by putting x=1, y=-1, z=m in the "homogeneous" (x,y,z) form of the HOMFLY polynomial: Del(L_+) - Del(L_-) = z.Del(L_0).


End of term HW schedule:

Let's say homework 6 is "officially" due next week (Mon March 4th) and HW 7 is "officially" due two weeks later, on Mon 18th (first day of exam week). I mean that those will be the dates on which Tom collects the work for marking, but by all means hand stuff in earlier for comments... just hand it in again the week after!

(I think this is the probably the best way to ensure that you can get as much feedback as possible but not be rushed into working on stuff I haven't lectured on yet!) 

Homework 7

6.1.2, 6.1.3, 6.2.7, 6.2.8, 6.2.12, 6.2.13, 6.2.14, 6.2.15. If you are careful about the first few, you should find it easier to be less careful about the later ones, which are more meant to get you used to some interesting behaviour of surfaces than as technical exercises!



Last update: Mon Feb 25