Odd covers of graphs
(with Calum Buchanan, Alexander Clifton, Eric Culver, Jiaxi Nie, Puck Rombach, Mei Yin) - Submitted (pdf)
Abstract: Given a finite simple graph \(G\), an odd cover of \(G\) is a collection of complete bipartite graphs, or bicliques, in which each edge of \(G\) appears in an odd number of bicliques and each non-edge of \(G\) appears in an even number of bicliques. We denote the minimum cardinality of an odd cover of \(G\) by \(b_2(G)\) and prove that \(b_2(G)\) is bounded below by half of the rank over \(\mathbb{F}_2\) of the adjacency matrix of \(G\). We show that this lower bound is tight in the case when \(G\) is a bipartite graph and almost tight when \(G\) is an odd cycle. However, we also present an infinite family of graphs which shows that this lower bound can be arbitrarily far away from \(b_2(G)\).
Babai and Frankl (1992) proposed the “odd cover problem,” which in our language is equivalent to determining \(b_2(K_n) \). Radhakrishnan, Sen, and Vishwanathan (2000) determined \(b_2(K_n)\) for an infinite but density zero subset of positive integers n. In this paper, we determine \(b_2(K_n)\) for a density \(3/8\) subset of the positive integers.
(with Calum Buchanan, Alexander Clifton, Eric Culver, Jiaxi Nie, Puck Rombach, Mei Yin) - Submitted (pdf)
Abstract: Given a finite simple graph \(G\), an odd cover of \(G\) is a collection of complete bipartite graphs, or bicliques, in which each edge of \(G\) appears in an odd number of bicliques and each non-edge of \(G\) appears in an even number of bicliques. We denote the minimum cardinality of an odd cover of \(G\) by \(b_2(G)\) and prove that \(b_2(G)\) is bounded below by half of the rank over \(\mathbb{F}_2\) of the adjacency matrix of \(G\). We show that this lower bound is tight in the case when \(G\) is a bipartite graph and almost tight when \(G\) is an odd cycle. However, we also present an infinite family of graphs which shows that this lower bound can be arbitrarily far away from \(b_2(G)\).
Babai and Frankl (1992) proposed the “odd cover problem,” which in our language is equivalent to determining \(b_2(K_n) \). Radhakrishnan, Sen, and Vishwanathan (2000) determined \(b_2(K_n)\) for an infinite but density zero subset of positive integers n. In this paper, we determine \(b_2(K_n)\) for a density \(3/8\) subset of the positive integers.
Towards supersaturation for oddtown and eventown
Submitted (pdf)
Abstract: Given a collection \(\mathcal{A}\) of subsets of an \(n\) element set, let \(\text{op}(\mathcal{A}) \) denote the number of distinct pairs \(A,B \in \mathcal{A} \) for which \(|A \cap B| \) is odd. Using linear algebra arguments, we prove that for any collection \(\mathcal{A}\) of \( 2^{\lfloor n/2 \rfloor}+1 \)even-sized subsets of an \(n \) element set that \( \text{op}(\mathcal{A}) \geq 2^{\lfloor n/2 \rfloor-1} \). We also prove that for any collection \( \mathcal{A} \) of \(n+1 \) odd-sized subsets of an \( n \) element set that \( \text{op}(\mathcal{A}) \geq 3 \), and that both of these results are best possible. We also consider the problem for larger collections of odd-sized and even-sized sets respectively.
Submitted (pdf)
Abstract: Given a collection \(\mathcal{A}\) of subsets of an \(n\) element set, let \(\text{op}(\mathcal{A}) \) denote the number of distinct pairs \(A,B \in \mathcal{A} \) for which \(|A \cap B| \) is odd. Using linear algebra arguments, we prove that for any collection \(\mathcal{A}\) of \( 2^{\lfloor n/2 \rfloor}+1 \)even-sized subsets of an \(n \) element set that \( \text{op}(\mathcal{A}) \geq 2^{\lfloor n/2 \rfloor-1} \). We also prove that for any collection \( \mathcal{A} \) of \(n+1 \) odd-sized subsets of an \( n \) element set that \( \text{op}(\mathcal{A}) \geq 3 \), and that both of these results are best possible. We also consider the problem for larger collections of odd-sized and even-sized sets respectively.
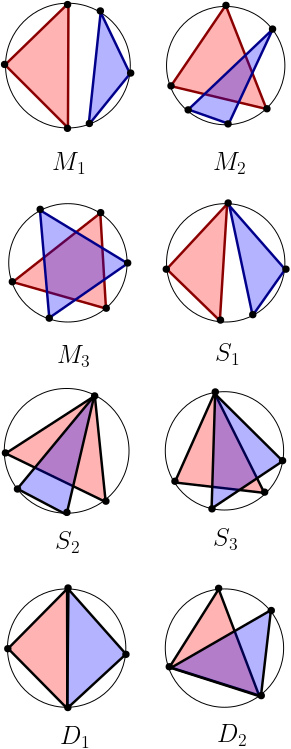
Saturation Problems in Convex Geometric Hypergraphs
(with Sam Spiro) - Submitted (pdf)
Abstract: A convex geometric hypergraph (abbreviated cgh) consists of a collection of subsets of a strictly convex set of points in the plane. Extremal problems for cgh's have been extensively studied in the literature, and in this paper we consider their corresponding saturation problems. We asymptotically determine the saturation number of two geometrically disjoint \(r\)-tuples. Further, amongst the eight nonisomorphic \(3\)-uniform cgh's on two edges, we determine the saturation number for seven of these up to order of magnitude and the eighth up to a log factor.
(with Sam Spiro) - Submitted (pdf)
Abstract: A convex geometric hypergraph (abbreviated cgh) consists of a collection of subsets of a strictly convex set of points in the plane. Extremal problems for cgh's have been extensively studied in the literature, and in this paper we consider their corresponding saturation problems. We asymptotically determine the saturation number of two geometrically disjoint \(r\)-tuples. Further, amongst the eight nonisomorphic \(3\)-uniform cgh's on two edges, we determine the saturation number for seven of these up to order of magnitude and the eighth up to a log factor.
A note on \(k\)-wise oddtown problems
(with Jacques Verstraete)
To appear in Graphs and Combinatorics (pdf)
Abstract: For integers \(2 \leq t \leq k\) , we consider a collection of \(k\) set families \( \mathcal{A}_j: 1 \leq j \leq k \) where \( \mathcal{A}_j = \{ A_{j,i} \subseteq [n] : 1 \leq i \leq m \} \) and \( |A_{1, i_1} \cap \cdots \cap A_{k,i_k}| \) is even if and only if at least \(t\) of the \(i_j \) are distinct. In this paper, we prove that \( m =O(n^{ 1/ \lfloor k/2 \rfloor})\) when \(t=k \) and \(m = O( n^{1/(t-1)})\) when \(2t-2 \leq k\) and prove that both of these bounds are best possible. Specializing to the case where \( \mathcal{A} = \mathcal{A}_1 = \cdots = \mathcal{A}_k\), we recover a variation of the classical oddtown problem.
(with Jacques Verstraete)
To appear in Graphs and Combinatorics (pdf)
Abstract: For integers \(2 \leq t \leq k\) , we consider a collection of \(k\) set families \( \mathcal{A}_j: 1 \leq j \leq k \) where \( \mathcal{A}_j = \{ A_{j,i} \subseteq [n] : 1 \leq i \leq m \} \) and \( |A_{1, i_1} \cap \cdots \cap A_{k,i_k}| \) is even if and only if at least \(t\) of the \(i_j \) are distinct. In this paper, we prove that \( m =O(n^{ 1/ \lfloor k/2 \rfloor})\) when \(t=k \) and \(m = O( n^{1/(t-1)})\) when \(2t-2 \leq k\) and prove that both of these bounds are best possible. Specializing to the case where \( \mathcal{A} = \mathcal{A}_1 = \cdots = \mathcal{A}_k\), we recover a variation of the classical oddtown problem.
Extremal problems for pairs of triangles
(with Zoltán Füredi, Dhruv Mubayi, Jacques Verstraete)
J. of Combin. Theory Series B, 155, 2022 - (Arxiv) and (Journal)
Abstract: A convex geometric hypergraph or cgh consists of a family of subsets of a strictly convex set of points in the plane. There are eight pairwise nonisomorphic cgh's consisting of two distinct triples. These were studied at length by Braß (2004) and by Aronov, Dujmović, Morin, Ooms, and da Silveira (2019). We determine the extremal functions exactly for seven of the eight configurations.
The above results are about cyclically ordered hypergraphs. We extend some of them for triangle systems with vertices from a non-convex set. We also solve problems posed by P. Frankl, Holmsen and Kupavskii (2020), in particular, we determine the exact maximum size of an intersecting family of triangles whose vertices come from a set of \(n\) points in the plane.
(with Zoltán Füredi, Dhruv Mubayi, Jacques Verstraete)
J. of Combin. Theory Series B, 155, 2022 - (Arxiv) and (Journal)
Abstract: A convex geometric hypergraph or cgh consists of a family of subsets of a strictly convex set of points in the plane. There are eight pairwise nonisomorphic cgh's consisting of two distinct triples. These were studied at length by Braß (2004) and by Aronov, Dujmović, Morin, Ooms, and da Silveira (2019). We determine the extremal functions exactly for seven of the eight configurations.
The above results are about cyclically ordered hypergraphs. We extend some of them for triangle systems with vertices from a non-convex set. We also solve problems posed by P. Frankl, Holmsen and Kupavskii (2020), in particular, we determine the exact maximum size of an intersecting family of triangles whose vertices come from a set of \(n\) points in the plane.
A generalization of Bollobás set pair inequality
(with Jacques Verstraete)
The Electronic Journal of Combinatorics, 28(3), 2021 - (Arxiv) and (Journal)
Abstract: The Bollobás set pairs inequality is a fundamental result in extremal set theory with many applications. In this paper, for \(n \geq k \geq t \geq 2 \), we consider a collection of \(k\) families \( \mathcal{A}_i: 1 \leq i \leq k\) where \( \mathcal{A}_i = \{ A_{i,j} \subset [n] : j \in [n] \}\) so that \[A_{1, i_1} \cap \cdots \cap A_{k,i_k} \neq \emptyset \] if and only if there are at least \(t\) distinct indices \( i_1,i_2,\dots,i_k \). Via a natural connection to a hypergraph covering problem, we give bounds on the maximum size \( \beta_{k,t}(n) \) of the families with ground set \( [n] \).
(with Jacques Verstraete)
The Electronic Journal of Combinatorics, 28(3), 2021 - (Arxiv) and (Journal)
Abstract: The Bollobás set pairs inequality is a fundamental result in extremal set theory with many applications. In this paper, for \(n \geq k \geq t \geq 2 \), we consider a collection of \(k\) families \( \mathcal{A}_i: 1 \leq i \leq k\) where \( \mathcal{A}_i = \{ A_{i,j} \subset [n] : j \in [n] \}\) so that \[A_{1, i_1} \cap \cdots \cap A_{k,i_k} \neq \emptyset \] if and only if there are at least \(t\) distinct indices \( i_1,i_2,\dots,i_k \). Via a natural connection to a hypergraph covering problem, we give bounds on the maximum size \( \beta_{k,t}(n) \) of the families with ground set \( [n] \).
Non-trivial \(d\)-wise intersecting families
(with Jacques Verstraete)
Journal of Combinatorial Theory Series A, 178, 2021 - (Arxiv) and (Journal)
Abstract: For an integer \(d \geq 2 \), a family \(\mathcal{F}\) of sets is \(d \)-wise intersecting if for any distinct sets \(A_1,A_2,\dots,A_d \in \mathcal{F} \), \(A_1 \cap A_2 \cap \dots \cap A_d \neq \emptyset \), and non-trivial if \(\bigcap_{A \in \mathcal{F}} A = \emptyset \). Hilton and Milner conjectured that for \( k \geq d \geq 2 \) and large enough \(n\), the extremal (i.e. largest) non-trivial \(d\)-wise intersecting family of \(k \)-element subsets of \([n] \)is, up to isomorphism, one of the following two families: \[ \mathcal{A}(k,d) = \{ A \in \textstyle{{[n] \choose k}} : |A \cap [d+1]| \geq d \} \] \[ \mathcal{H} (k,d) = \{A \in \textstyle{{[n] \choose k}} : [d-1] \subset A, A \cap [d,k+1] \neq \emptyset\} \cup \{[k+1] \setminus \{i \} : i \in [d - 1]\}. \] The celebrated Hilton-Milner Theorem states that \(\mathcal{H}(k,2)\) is the unique, up to isomorphism, extremal non-trivial intersecting family for \(k>3\). We prove the conjecture and prove a stability theorem, stating that any large enough non-trivial \(d\)-wise intersecting family of \(k\)-element subsets of \([n]\) is a subfamily of \( \mathcal{A}(k,d) \) or \(\mathcal{H}(k,d)\).
(with Jacques Verstraete)
Journal of Combinatorial Theory Series A, 178, 2021 - (Arxiv) and (Journal)
Abstract: For an integer \(d \geq 2 \), a family \(\mathcal{F}\) of sets is \(d \)-wise intersecting if for any distinct sets \(A_1,A_2,\dots,A_d \in \mathcal{F} \), \(A_1 \cap A_2 \cap \dots \cap A_d \neq \emptyset \), and non-trivial if \(\bigcap_{A \in \mathcal{F}} A = \emptyset \). Hilton and Milner conjectured that for \( k \geq d \geq 2 \) and large enough \(n\), the extremal (i.e. largest) non-trivial \(d\)-wise intersecting family of \(k \)-element subsets of \([n] \)is, up to isomorphism, one of the following two families: \[ \mathcal{A}(k,d) = \{ A \in \textstyle{{[n] \choose k}} : |A \cap [d+1]| \geq d \} \] \[ \mathcal{H} (k,d) = \{A \in \textstyle{{[n] \choose k}} : [d-1] \subset A, A \cap [d,k+1] \neq \emptyset\} \cup \{[k+1] \setminus \{i \} : i \in [d - 1]\}. \] The celebrated Hilton-Milner Theorem states that \(\mathcal{H}(k,2)\) is the unique, up to isomorphism, extremal non-trivial intersecting family for \(k>3\). We prove the conjecture and prove a stability theorem, stating that any large enough non-trivial \(d\)-wise intersecting family of \(k\)-element subsets of \([n]\) is a subfamily of \( \mathcal{A}(k,d) \) or \(\mathcal{H}(k,d)\).
On the poset and asymptotics of Tesler matrices
The Electronic Journal of Combinatorics, 25(2), 2018 - (Arxiv) and (Journal)
Abstract: Tesler matrices are certain integral matrices counted by the Kostant partition function and have appeared recently in Haglund’s study of diagonal harmonics. In 2014, Drew Armstrong defined a poset on such matrices and conjectured that the characteristic polynomial of this poset is a power of \(q−1\). We use a method of Hallam and Sagan to prove a stronger version of this conjecture for posets of a certain class of generalized Tesler matrices. We also study bounds for the number of Tesler matrices and how they compare to the number of parking functions, the dimension of the space of diagonal harmonics.
The Electronic Journal of Combinatorics, 25(2), 2018 - (Arxiv) and (Journal)
Abstract: Tesler matrices are certain integral matrices counted by the Kostant partition function and have appeared recently in Haglund’s study of diagonal harmonics. In 2014, Drew Armstrong defined a poset on such matrices and conjectured that the characteristic polynomial of this poset is a power of \(q−1\). We use a method of Hallam and Sagan to prove a stronger version of this conjecture for posets of a certain class of generalized Tesler matrices. We also study bounds for the number of Tesler matrices and how they compare to the number of parking functions, the dimension of the space of diagonal harmonics.