The Stomachion is perhaps the world's oldest puzzle. It is often attributed to (or
thought to have been invented by)
Archimedes of
Syracuse (287 BC - 212 BC).
It is a
geometric game and is often referred to as the
"Loculus of Archimedes" (Archimedes' box).
There is a truly amazing story about
Archimedes' scrolls, the
Palimpsest, which was cut up,
written over and eventually recovered through a journey of more than two thousand years.
There are many excellent websites containing fascinating historical
aspects of the Stomachion. This website mainly deals with combinatorial problems that are
associated with
the Stomachion. A tour (in fact, a so-called traveling-salesman tour) is illustrated through almost all
solutions
of dissecting the square by Archimedes' pieces. A number of problems
concerning the Stomachion are also mentioned.
We point out that there is some evidence that the Stomachion shape may have
actually been a 2 by 1 rectangle, rather than a square, with the 14 pieces
stretched accordingly (e.g., see the
letter
by R. D. Oldham in Nature 117, no. 2940, (1926), pp 337--338, or his
article in
New York Times
August 1, 1926).
The original Stomachion consists of 14 pieces that tile a square as illustrated in one such example
below.
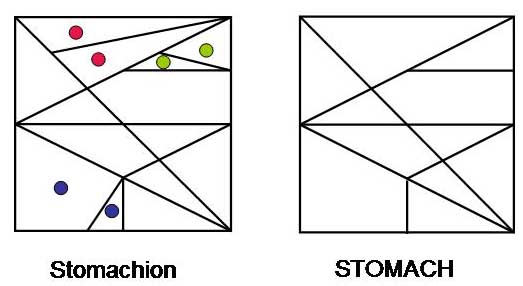 However, it can be shown that the two tiles with red dots must be bound together
in any tiling of the square.
So must the two with green dots and the two with blue dots as well. At our request,
George Miller made
a game set of
11 pieces. This modified puzzle
is called STOMACH (three characters fewer than the original).
Well, the word Stomachion has its root in a Greek word,
στομα'χιον, meaning stomach, anyway.
However, it can be shown that the two tiles with red dots must be bound together
in any tiling of the square.
So must the two with green dots and the two with blue dots as well. At our request,
George Miller made
a game set of
11 pieces. This modified puzzle
is called STOMACH (three characters fewer than the original).
Well, the word Stomachion has its root in a Greek word,
στομα'χιον, meaning stomach, anyway.
Problem 1: How many different solutions are there for STOMACH?
(How many different ways are there to tile
a square by using these "reduced" pieces?)
The answer to this question depends on what one means by "different". If we do not
distinguish between congruent tiles, then the answer is 2144 (= 8 x 268).
If further, we identify two tilings that differ only by rotations and/or reflections the number is 268. On the other hand, if we distinguish both of
these possibilities, then the grand total is 17152. Bill Cutler first computed that there are
536 (= 2 x 268) equivalent tilings using the original Stomachion tiles, up to
rotation and reflection. Of course, one tile in one of the Stomach identical pairs is made of two tiles in the original Stomachion puzzle.
(More on reduction by symmetries.)
Problem 2: Can we reach any configuration from any other by "simple" moves?
By a simple move, we mean flipping or rotating a symmetric sub-region formed by a set of contiguous STOMACH pieces.
To
solve Problem 2, we form a graph with a vertex set consisting of 268 nodes each corresponding
to a unique solution to STOMACH. Two vertices are said to be adjacent to each other if there
is a "simple" move transforming one to the other.
Problem 2 can be rephased as "Is the STOMACH graph connected?"
The answer to Problem 2 is almost, but not quite, yes. As it turns out, the STOMACH graph has
a giant connected component of 266 vertices and a minor component of 2 vertices, illustrated below.
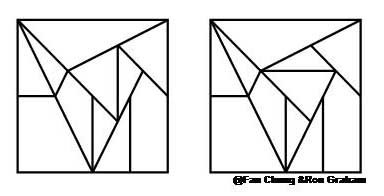 Problem 3: Is there an efficient tour of all the tilings for STOMACH?
Problem 3: Is there an efficient tour of all the tilings for STOMACH?
Here we give a Hamiltonian cycle (i.e., a cycle containing each vertex exactly once
and returning to the original starting point) of the giant component
of 266 vertices. From any starting configuration, by clicking at "next", you will get
a configuration that differs only by a simple move. After 266 clicks, you will have seen
all the 266 configurations in the giant component and will have returned to the starting configuration.
Click here for a tour of STOMACH.
Problem 4: What are some interesting properties of the STOMACH graph?
We have computed some basic facts about the STOMACH graph.
-
The STOMACH graph has 268 vertices and 937 edges.
-
There are 936 edges in the giant component of the STOMACH graph.
-
The diameter of the giant component of the STOMACH graph is 11.
-
The super graph with 17152 stomachion tilings has diameter 15 in its giant component.
-
More

 However, it can be shown that the two tiles with red dots must be bound together
in any tiling of the square.
So must the two with green dots and the two with blue dots as well. At our request,
George Miller made
a game set of
11 pieces. This modified puzzle
is called STOMACH (three characters fewer than the original).
Well, the word Stomachion has its root in a Greek word,
στομα'χιον, meaning stomach, anyway.
However, it can be shown that the two tiles with red dots must be bound together
in any tiling of the square.
So must the two with green dots and the two with blue dots as well. At our request,
George Miller made
a game set of
11 pieces. This modified puzzle
is called STOMACH (three characters fewer than the original).
Well, the word Stomachion has its root in a Greek word,
στομα'χιον, meaning stomach, anyway.
