
 Math 262
Math 262
A few words on research for graduate students
Fan Chung Graham
(professional name:
Fan Chung ,
Chinese name 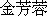 )
is the Paul Erdos Professor in Combinatorics
at UC San Diego.
Previously, she
had taught
at U Penn, worked
at Bell
Labs (in its glory old days), and directed some great research groups
at Bellcore.
)
is the Paul Erdos Professor in Combinatorics
at UC San Diego.
Previously, she
had taught
at U Penn, worked
at Bell
Labs (in its glory old days), and directed some great research groups
at Bellcore.
Her research interests are primarily in graph theory, combinatorics and algorithmic design.
In particular, she is known for her work in the following
areas:
- Spectral graph theory
.
In her book
Spectral Graph Theory, a normalized and powerful Laplacian for gener
al
graphs was introduced and examined.
The eigenvalues of the Laplacian
capture fundamental properties of a graph/network and
have connections with
the pure (spectral geometry, extremal graph theory, representation theory, etc)
and the applied (Markov chains, approximation algorithms,
segmentation, computer vision, Internet algorithms, etc).
She has recently been working on spectral aspects of directed graphs.
-
Random
graphs
with general degree distribution
with applications to complex networks.
Graph theory has emerged as a primary tool for detecting numerous
hidden structures in various information networks, including
Internet graphs, social networks, biological networks, or
any graph representing relations in massive data sets.
One of the main tools is
random graph theory for general degree distributions.
On this topic, here is a
survey and a book
Complex graphs and networks
coauthored with Lincoln Lu published by AMS, based
on ten lectures
given at
the
CBMS Workshop on
"The Combinatorics of Large Sparse Graphs"
.
Also there is
the journal
Internet Mathematics
,
for which she serves as the
Editor-in-Chief. Her on-going research
focuses on exploring the structure of large
random-like graphs and the relationship with its subgraphs as well as developing
efficient local algorithms.
-
Quasi-randomness.
A large family of graph properties, all of which
are shared by random graphs, were shown to be equivalent in the sense that if a
graph satisfies one of the properties, it must satisfy all of them.
The list of equivalent graph properties includes some hard-to-compute
properties such as the expansion property,
the discrepancy property, subgraph enumeration properties as well as some easy-
to-compute
properties such as the eigenvalue property and four-cycle properties.
This
provides a validation scheme for
approximating one graph property by using other equivalent properties.
The theory of quasi-randomness
was introduced through
a
series of papers and recently has been further developed.
(The recently defined "XOR product" was introduced as the box-product in a paper in 1991, which also
contains
the often used and misquoted
"octahedrons" of hypergraphs.)
Some of her recent work include
sparse quasi-random graphs for graphs with general degree distribution.
-
 Unavoidable graphs and
universal graphs .
A basic question in extremal graph theory is to find unavoidable
patterns and structures in graphs with given density or distribution. A complementary problem
is to find a smallest graph which contains
a given family of graphs as subgraphs.
These topics can be viewed as extensions of
Ramsey theory, one of her favorite subject. Her
lower bounds for the Ramsey number r(3,3,...,3) from her thesis is still the best known so far.
She also has done research on the
graph diameter,
average distance, and
graph embeddings as well as their applications in
parallel computing, and
communication networks.
Unavoidable graphs and
universal graphs .
A basic question in extremal graph theory is to find unavoidable
patterns and structures in graphs with given density or distribution. A complementary problem
is to find a smallest graph which contains
a given family of graphs as subgraphs.
These topics can be viewed as extensions of
Ramsey theory, one of her favorite subject. Her
lower bounds for the Ramsey number r(3,3,...,3) from her thesis is still the best known so far.
She also has done research on the
graph diameter,
average distance, and
graph embeddings as well as their applications in
parallel computing, and
communication networks.
Recently, she has been working on
several interrelated topics including:
Other topics that she has investigated now and then include:
|
discrete geometry|
algorithms|
Steiner trees|
Buckyball|
hypercubes|
codes|.
She has written over 240
papers
and
has
about 120
coauthors.
In addition to Spectral Graph Theory and
Complex Graphs and Networks (coauthored with Lincoln Lu), she has a third book
Erdös on Graphs,
coauthored with Ron Graham.
She serves on the editorial boards of a dozen or so journals.
In 1990, she was awarded the Allendoerfer Award by Mathematical Association of America.
In 1994, she gave an invited talk at the International Congress of
Mathematicians (ICM) in Zürich.
Since 1998, she has been a fellow of American Academy of Arts and Sciences.
Related links:







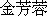 )
is the Paul Erdos Professor in Combinatorics
at UC San Diego.
Previously, she
had taught
at U Penn, worked
at Bell
Labs (in its glory old days), and directed some great research groups
at Bellcore.
)
is the Paul Erdos Professor in Combinatorics
at UC San Diego.
Previously, she
had taught
at U Penn, worked
at Bell
Labs (in its glory old days), and directed some great research groups
at Bellcore.
 Unavoidable graphs and
universal graphs .
A basic question in extremal graph theory is to find unavoidable
patterns and structures in graphs with given density or distribution. A complementary problem
is to find a smallest graph which contains
a given family of graphs as subgraphs.
These topics can be viewed as extensions of
Ramsey theory, one of her favorite subject. Her
lower bounds for the Ramsey number r(3,3,...,3) from her thesis is still the best known so far.
She also has done research on the
graph diameter,
average distance, and
graph embeddings as well as their applications in
parallel computing, and
communication networks.
Unavoidable graphs and
universal graphs .
A basic question in extremal graph theory is to find unavoidable
patterns and structures in graphs with given density or distribution. A complementary problem
is to find a smallest graph which contains
a given family of graphs as subgraphs.
These topics can be viewed as extensions of
Ramsey theory, one of her favorite subject. Her
lower bounds for the Ramsey number r(3,3,...,3) from her thesis is still the best known so far.
She also has done research on the
graph diameter,
average distance, and
graph embeddings as well as their applications in
parallel computing, and
communication networks.