Rob's Homepage

Tuan's Homepage

Math 152 Web Page

I.Introduction:

In this assignment, we will figure out the cutwidth of some simple graphs: complete graphs, cycles, n-cubes and tree. Also we will create an algorithm that chooses the best layout with minimum cutwidth of a graph.

II. Definition of the Cutwidth of a Graph:[1]

For a given graph G=(V,E), consider labelings that assign each vertex a distinct number from 1 to n where |V|=n. For each labeling f, the cutwidth c(f) of f is the maximum value of |{(u,v) in E:f(u)<=i< f(v) }|for i=1,..., n-1. The cutwidth c(G) of the graph G is the minimum value of c(f) where f ranges over all labelings of G. In other words, c(G) = min {c(f) : f is a labeling of G}.

III. Examples:

We find the cutwidth of different graphs as follows:

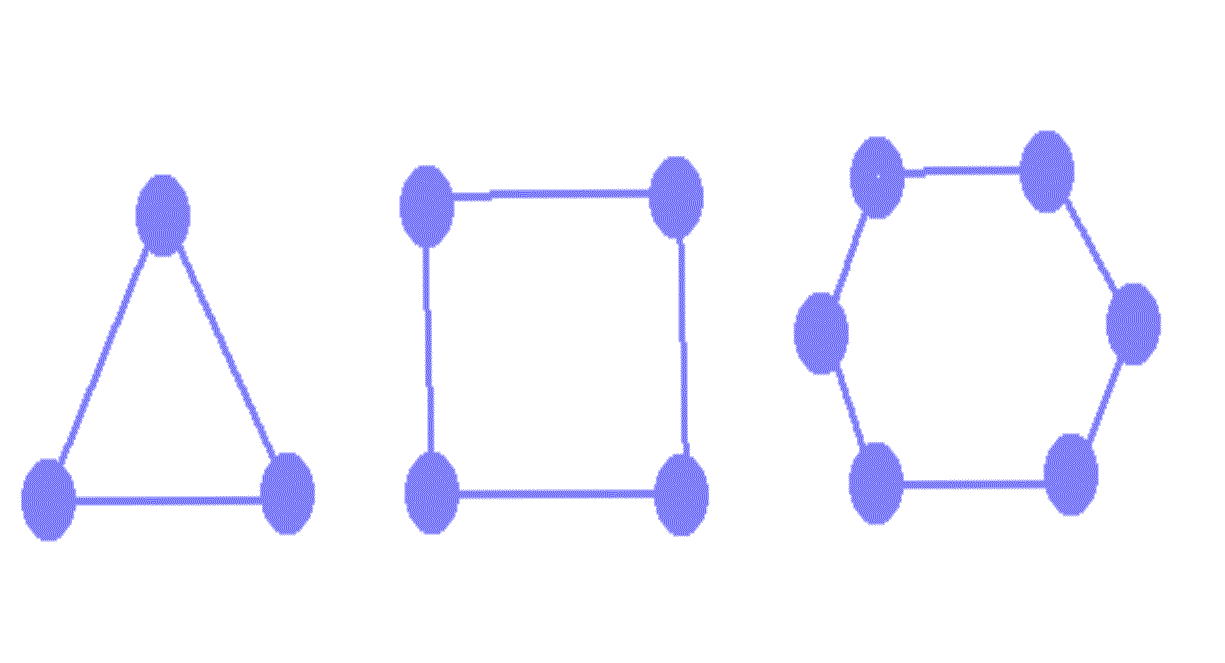
1. The Cycles Cn: The cycle Cn, n>=3, consists of n vetices v1, v2,...,vn and edges {v1,v2}{v2,v3}...{vn-1,vn} and {vn,v1}. The cycles C3, C4 and C5 are displayed below.
* The cutwidth of C3:
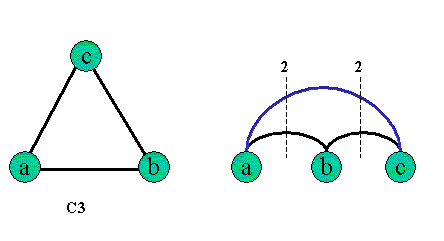
From the above figure, we easily figure out the cut width of C3 is 2.
* The cutwidth of C4:
We have two different layouts for C4.

+Layout f1:
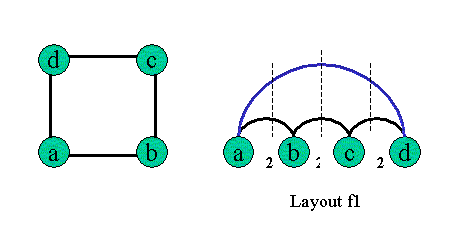
f1:..... (1)..... (2)..... (3)
cuts:..... 2....... 2....... 2
=>c(f1) = 2;
+Layout f2:
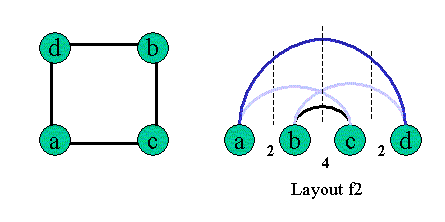
f2:.....(1).....(2).....(3)
cuts:......2......4......2
=>c(f2) = 4;
From definition, we have:
cw(f) = max all cuts (size of cuts);
cw(f1) = max {2, 2, 2} = 2;
cw(f2) = max {2, 4, 2} = 4;
--------------------------------
=> cw(G)= min of all layouts {cw(f)} = min {2, 4} = 2;
We can conclude that the cutwidth of a Cn graph is always 2 because there exists a layout that all the sizes of cuts are 2 in which one vertex connected with two adjacent vertices and two vertices at both ends are connected together.

2. The Complete Graph Kn:The complete graph Kn with n>=3 is a simple graph that contains exactly one edge between each pair of distinct vertices.

* The Cutwidth of K3: the cutwidth of K3 is exactly the same as cutwidth of C3 that is cw(G) = 2;
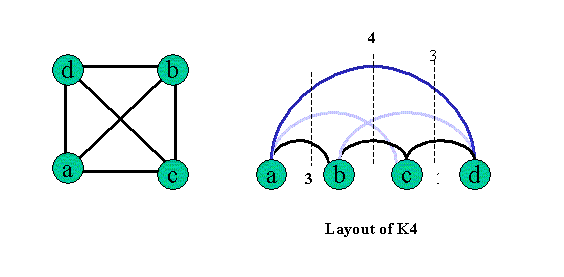
* The Cutwidth of K4: from the figure below, we find out the cutwidth of K4 is cw(G) = 4;

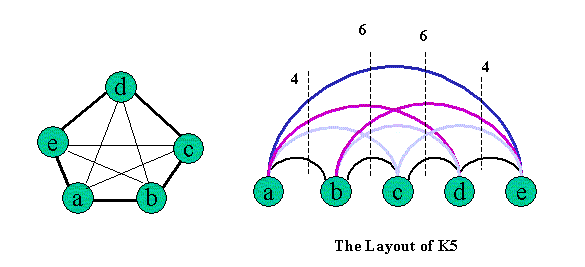
* The Cutwidth of K5: from the figure below, we find out the cutwidth of K5 is cw(G) = 6;

From the above results, we notice that:

When the number of vertices n = 3, the cutwidth cw(G) = 2;
When the number of vertices n = 4, the cutwidth cw(G) = 4;
When the number of vertices n = 5, the cutwidth cw(G) = 6;
Therefore, we guess that the formula for the cutwidth of a Kn is cw(G) = 2n - 4;
And the largest cut is always in the middle of the layout at the position ceiling of [n/2].

3. The n-Cubes:a Qn is a simple graph that has n vertices which labeled by the power n of 2 bit strings of lenght n. Two vertices are adjacent if and only if the bit strings that they labeled differ in exactly one bit. The graphs of Q1, Q2 and Q3 are displayed below:

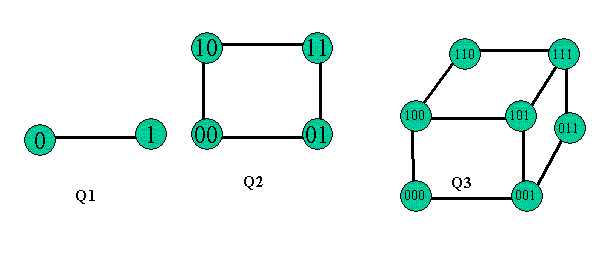
* The cutwidth of Q1: we can easily regconize that the cutwidth of Q1 is cw(G) = 1;
* The cutwidth of Q2: Q2 has the same cutwidth as C2 that is cw(G) = 2;
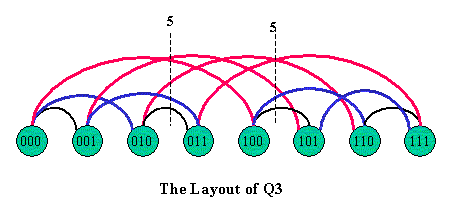
* The cutwidth of Q3; from the figure below, we can find out the cutwidth of Q3 is cw(G) = 5;

4. The Cutwidth of a Tree: we use an example described by Chung [2].

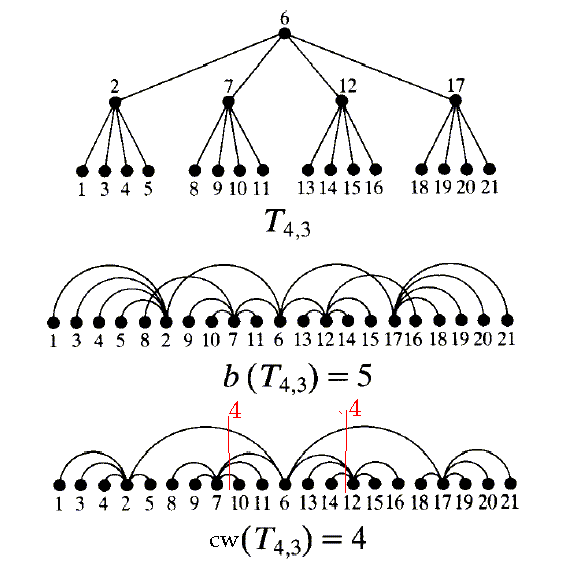
Lengauer [3] proved that the cutwidth for the complete k-level t-ary trees Tk,t evaluated by this formula:
cw(Tt,k) = ceiling of|1/2(k - 1)(t - 1)| + 1, for k >= 3 ||
Applying this formula we can easily figure out the cutwidth of T(4,3):
cw(T4,3) = ceiling of[1/2(3 - 1)(4 - 1)] + 1 = ceiling of[1/2 (2) (3)] + 1 = 4;

IV. Algorithm for the Cutwidth:
Algorithm: to evaluate the cutwidth of a graph.
Input: G [ a graph with n vertices ].
Body:[ build a layout consisting all the vertices of G then switch all pairs of { i, j } of vertices until getting a layout with a minimum cutwidth ].

1. Initial layout f with cutwidth cw.
2. While(there exists a better layout f' with smaller cutwidth cw')

2a. Looking for a better layout f'.

if (cutwidth cw' < cw)

replace f by f';

else

loop again on all pairs { i,j } of vertices;

2b. End while: can not find a better layout.

3. Output: layout f as best layout found with minimum cutwidth cw.

end algorithm.

We apply this algorithm to find the cutwidth of C4. After switching the vertices around, we have 2 different layouts with the cutwidth of 2 and 4; and after running this algorithm we pick out one of the layout with cutwidth equals 2 as the best layout found.

V. Applications of the Cutwidths:

The concept of the cutwidth has been applied in many fields:

1. The Cyclic Cutwidth of the Mesh: The cutwidth problem is to find a linear layout so that the number of cuts (cw) is minimized. The cyclic cutwidth deals with a circular layout with cyclic cutwidth (ccw) (Cyclic Cutwidth of the Mesh)
2. VSLI Design: The cutwidth concept often relates to the area of the layout in VLSI design. The Harvard VLSI Research Group is involved in the design and analysis of a variety of digital, analog and Mix-Signal VLSI System.(Harvard VLSI Lab)
3. The Cavity Structure Design: A constant gradient stucture has been devised by introducing a cut between the adjacent cavity cells along the beam axis of each haft structure. The width of the cut is varied along the longitudinal axis of the structure to have proper coupling between the cells(A Constant Gradient Planar Accelerating Stucture for Linac Use).

VI. Links:
There are some gook links to the cutwidth:

1. Labelings of Graphs
2. Cutwidth Reference
3. Contructive linear time algorithms for small cutwidth and carving-width

VII. Conclusion:
The cutwidth of a layout is the maximum number of cuts between succesive vertices in a linear layout. The cutwidth of a graph is the minimum cutwidth over all possible layouts. The concept of the cutwidth has been applied in many different fields of Mathematics and Computer Science for a variety of reasons.

Reference

[1], Final Projects

[2], Labelings of Graphs

[3], T. laenganuer, Upper and lower bounds on the complexity of the min-cut linear arrangement problem on trees, SIAM J. Alg. Discrete Methods 3 (1982), 99-113;MR83a:68081.

[4], Tools for Creating Heuristics

top
home