Created by Jennifer Bakker
Spring 2004
Math 187
Professor: O'Bryant
There are several variations of the knapsack problem that are relevant in the fields of complexity theory, applied mathematics and cryptography. For our purposes, we will mainly be concerned with its application in cryptography. The reason why knapsack systems are pertinent is because the encryption process is very fast, in fact, faster than RSA.
The problem goes like this...There is a thief ![]() who breaks into a jewelry store which is showcasing various gems
who breaks into a jewelry store which is showcasing various gems ![]() . Each gem has a weight and is appraised to be worth a certain value. If the thief wants to fill his knapsack, which gems should he steal in order to maximize the cumulative value?
. Each gem has a weight and is appraised to be worth a certain value. If the thief wants to fill his knapsack, which gems should he steal in order to maximize the cumulative value?
Here is a simple applet simulating the knapsack problem, where c = capacity, p = price, w = weight and x = 0 or 1 (in or out). Click link #5.
A special case of this problem occurs when the value of each gem is equal to its size and then finding a subset of the gems that sum to a given capacity. This is commonly known as the "subset sum problem" or "knapsack problem" in cryptography. It is possible that no such subset exists or that the number of gems is so great that the worst case scenario is too difficult to solve; therefore, the problem is NP-complete. This problem generalizes to other NP-complete problems, in particular, the Traveling Salesman Problem (TSP).
One of the earliest public key cryptosystems is the knapsack cryptosystem, first described by Ralph Merkle & Martin Hellman in 1978 and the underlying scheme implements the subset sum problem. As stated before, the subset sum problem can be unsolvable, however, there are still instances of the problem that are solvable. The basic idea of the Merkle-Hellman scheme is in transforming hard or unfeasible subset sum problems into easy subset sum problems.
Suppose Bob wants to send a message to Alice, and Alice's public key is a = (a1, a2, ..., an). To encipher a message x = (x1, x2, ..., xn) of n bits, Bob makes the sum:
![]() (1)
(1)
S is then sent to Alice. If the message is long it can be split up into blocks of n bits, padding the last block with zeros if necessary. Since the enciphering key is made public and S can potentially be eavesdropped, then extracting x from S and a should intentionally be hard. If a is chosen to be a sequence of integers, then Alice can usually not find x in a reasonable amount of CPU time or the task is just NP-hard. This is because the only way to find x is to try all 2n possible values of x if equation 1 is satisfied, which is unfeasible if n is say greater than 100. This makes eavesdropping a somewhat trivial concern and consequently making it even harder to find x.
If a is chosen randomly by Alice, it will also be hardly possible for her to decipher S and find the plaintext x. This is where the Merkle-Hellman trapdoor comes into play. It allows Alice to overcome the infeasibility of finding x given S and gives her some secret information. The secret information is called the deciphering key. The trapdoor information is taken into consideration when Alice creates her public key. As it turns out, it is precisely the use of the trapdoor technique that makes the scheme insecure.
It should be noted that S must be a one-to-one function because if there are two different plaintexts x and y that give the same ciphertext, the receiver cannot uniquely recover the plaintext. It then must be determined how to generate a one-to-one enciphering key which, in general, is a co-NP-complete problem. However, the trapdoor has a way around this.
When Alice constructed her public enciphering key a, she first generated a super-increasing sequence of natural numbers ![]() . The vector
. The vector ![]() is said to be a super increasing sequence if for each i, with
is said to be a super increasing sequence if for each i, with ![]() ,
,
![]()
In words, a super-increasing sequence is when each term is greater than the sum of the previous terms. For example, (1, 2, 4, 8, ..., 2n-1) is a super-increasing sequence and is considered an "easy" sequence and (1, 2, 3, 4, 5,...,9) is not a super-increasing sequence. To determine if a sequence is super- increasing a computer only has to make one pass over the whole sequence which takes O(h) time. So in deciding whether a subset sum, T, is part of a super- increasing set, the computer must find the largest number in the set less than or equal to T and subtract it to get T'. It repeats this process with T'. If T' ends up to be zero, then the subset sum consists of all the numbers subtracted from T.
Hiding the "easy" super-increasing sequence from eavesdroppers involves performing several modulo transformations. The transformations are of the following type:
![]() (2)
(2)
![]() (3)
(3)
![]() and
and ![]() , (4)
, (4)
or ![]() and
and ![]() ,
,
When k transformations are used, the public key a is equal to ![]() . Equation 2 is called the Merkle-Hellman dominance and equations 4 is the Merkle-Hellman transformation. When using the transformations in the direction of aj+1 to aj it is called the reverse Merkle-Hellman transformation. If one transformation is used then it is called a basic or single iterated scheme (we also drop the indices j, j + 1, k, and k + 1) and if two transformations are used then it is called a double iterated scheme.
. Equation 2 is called the Merkle-Hellman dominance and equations 4 is the Merkle-Hellman transformation. When using the transformations in the direction of aj+1 to aj it is called the reverse Merkle-Hellman transformation. If one transformation is used then it is called a basic or single iterated scheme (we also drop the indices j, j + 1, k, and k + 1) and if two transformations are used then it is called a double iterated scheme.
To decipher the encrypted message, Alice must calculate ![]() using S and the deciphering key, where
using S and the deciphering key, where
![]() and
and ![]() (5)
(5)
So letting h = n, if ![]() , then xh has to be one, otherwise it is zero. Then Alice continues iteratively, subtracting xhah from S1, with h decrementing from n to 1 during the iterations.
, then xh has to be one, otherwise it is zero. Then Alice continues iteratively, subtracting xhah from S1, with h decrementing from n to 1 during the iterations.
A poset or partially ordered set is a set taken together with a partial order on it. To illustrate the point, let A and B be two sets, A is a subset of B, then these sets are partially ordered with respect to eachother. If A is not a subset of B and B is not a subset of A, then they are not partially ordered.
To look at an example of the lattice formed by the power set of {a,b,c}, refer to this link.
The LLL algorithm was first realized in the 1980s by Lenstra, Lenstra, and Lovasz. Its original intent was not to break any cryptosystems, but to factor polynomials with rational coefficients. It also improved upon the lattice reduction algorithm in order to solve integer linear programming. Later it was adapted for use in crypanalysis.
Before giving an explanation of the LLL algorithm, lets define a lattice in a more useful way. Let (v1,...vn) be a linearly independents set of real vectors in a n-dimensional real Euclidean space. The set of all points u1v1+...+unvn with integral u1,...un is called the lattice with basis (v1,....,vn).
Theorem
Let (v1,...,vn) be a basis of a lattice L and let v'i be the points
![]() for
for ![]() and
and ![]()
where zij are integers, the the set (v'1,...,v'n) is also a base for the same lattice L, if and only if det(zij) = +/- 1. We call an integer matrix Z with det (zij) = +/- 1 an unimodular matrix. [End Theorem]
Consequently, the |det(v1,...,vn)| is independent of a particular basis for a lattice.
It is common for basises for lattices to sometimes have large coefficients because according to the geometric theory of numbers there does not exist a set of n vectors such that they form an orthogonal set. The LLL algorithm finds, in polynomial time, a basis for a lattice L, which is nearly orthogonal with respect to a certain measure of non-orthogonality. A basis is called reduced if it contains relatively short vectors and that is what the theorem above does, find short vectors. These are not guaranteed to be the shortest vectors, but its length will not exceed the length of the shortest vector by more than a multiplicative constant.
Let v1,....,vn belong to the n-dimensional real vector space. To initialize the algorithm a orthogonal real basis v'i is calculated, together with ![]() , such that
, such that
![]() (6)
(6)
![]() (7)
(7)
where * denotes the inner scalar product. In the course of the algorithm the vectors v1,v2...,vn will be changed several times, but will always remain a basis for L. After every change the v'i and mij are updated using equations 6 and 7. A current subscript k is used during the algorithm. LLL starts with k = 2. If k = n + 1 it terminates. Suppose now k <= n, then we first want |mkk-1| <= 1/2 if k > 1. If this does not hold, let r be the integer nearest to mkk-1 and replace vk by vk - rvk-1, (don't forget the update). Next we distinguish two cases. Suppose that k >= 2 and |v'k + mkk-1v'k-1| < (3/4)|v'k-1|2, then we interchange vk-1 and vk, (don't forget the update), afterwards replace k by k - 1 and restart. In the other case we want
![]() for
for ![]() (8)
(8)
If the condition in equation 8 does not hold, then let l be the largest index < k with mlk > 1/2, let r be the nearest to mlk and replace bk by bk - rbl, (don't forget the update), repeat until the conditions in equation 8 hold, afterwards replace k by k + 1 and restart. Note if the case k = 1 appears one replaces it by k = 2.
Mathematica can implement the LLL algorithm by calling the function LatticeReduce[matrix]. Note that the input must consist of rational numbers.
Public knapsack:
We are going to encrypt 101100111 as 575 + 1586 + 1030 + 721 + 1183 + 1570 = 6665. The receiver computers 6665 * 317 mod 2003 = 1643 and uses S to find the plaintext. This is done by constructing the binary string from right to left: 1643 - 946(1) = 697; 697 - 450(1) = 247; 247 - 215(1) = 32; 32 - 45(0) = 32; 32 - 21(1) = 11; 11 - 9(1) = 2; 2 - 5(0) = 2; 2 - 2(1) = 0. We get back the original plaintext 101100111.
An attacker knows:
The attacker wants to find xi in {0, 1} such that 575x0 + 436x1 + 1586x2 + 1030x3 + 1921x4 + 569x5 + 721x6 + 1183x7 + 1570x8 = 6665. This can be written as T * X = 6665. Lets rewrite the problem as M * V = W where
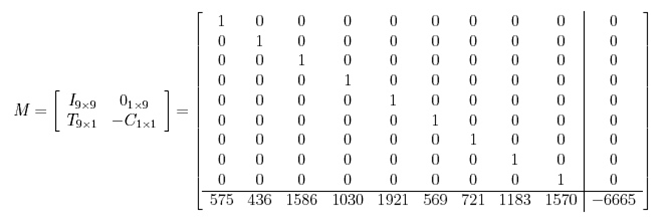
The solution is the short vector in the lattice spanned by the columns of M and this is where we use the LLL algorithm to find the solution. Matrix M' is the result of applying LLL to M
____________________________________@_________________
The column marked with a "@" has the right form so the likely solution is 101100111, which is absolutely correct!
After the realization of the LLL algorithm, subsequent modifications have been applied to the knapsack scheme, attempting to improve its security. But as the knapsack scheme evolved so did the LLL algorithm, in particular, that proposed by Schnorr. Shamir is the first to actually apply the LLL algorithm to break the Merkle-Hellman cryptosystem using Lenstra's linear programming algorithm and later Adleman extended his work by treating the cryptographic problem as a lattice problem rather than a linear programming problem. Even further improvements were made until every known trapdoor knapsack public key scheme had been broken, the last being the Chor-Rivest scheme and the general knapsack scheme.
Other uses of the knapsacks in cryptography include use of knapsacks (subset sum) problem as a one-way function instead of the S-Boxes in DES, proposed by Desmedt, Vandewalle and Govaerts. Also Shamir has come up with a "provably" secure protocol to protect passports.
It seems that there is little security using any trapdoor knapsack based cryptosystem for protecting signatures and authenticity. There might, however, be a future for it in other scientific applications, for example, protocols which is a standardized means of communication among machines across a network. Of course research into this idea would involve a completely different approach.
Desmedt, Y.G., Skwirzynski, J.K. ed, What happened to the knapsack cryptographic scheme?, Vol. 142, Netherlands: Kluwer Academic Publishers 1988
Joux, Antoine and Stern, Jacques, "Lattice Reduction: a Toolbox for the Cryptanalysis." Diss. Laboratoire d'Informatique Ecole Normale Superieure, Paris, 1994
Washington University, <http://www.cs.washington.edu/homes/cary/lattice.pdf>, Last Accessed: 6/10/04
Rutgers University, <http://www.rci.rutgers.edu/%7ecfs/305_html/Induction/Lattices.html#anchor2384323>, Last Accessed: 6/10/2004
Micciancio, Daniele, CSE207C, UCSD, <http://www.cs.ucsd.edu/%7Edaniele/CSE207C/>, Last Accessed: 6/9/2004
Kallen, William van der, Mathematisch Instituut Universiteit Utrecht, <http://www.math.uu.nl/people/vdkallen/lllimplementations.html>, Last Accessed: 6/9/2004
The Free Dictionary, <http://encyclopedia.thefreedictionary.com/Knapsack%20problem>, Last Accessed: 6/8/2004
Wolfram, MathWorld, <http://mathworld.wolfram.com/LLLAlgorithm.html>, Last Accessed: 6/7/2004
Additional References that I didn't use but might be of interest can be found here.